Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

МЕТОДЫ ФОТОМЕТРИЧЕСКОГО АНАЛИЗА В САНИТАРНО-ГИГИЕНИЧЕСКИХ ИССЛЕДОВАНИЯХ

Дорогова В Б, Игнатьева Л П,

4.4.1. Расчет линейного градуировочного графика у = а + bх и метрологических характеристик его параметров

Линейное уравнение связи двух переменных (парную линейную регрессию) можно представить в виде:

Y = ?0 + ?х, (4.21)

где ?0 + ? – неизвестные параметры (коэффициенты) регрессии.

Задача сводится к определению значений ?0 + ?. Истинные значения этих параметров найти нельзя, так как объем выборки экспериментальных данных ограничен. Поэтому рассчитанные значения параметров являются статистическими оценками истинных параметров. Эти оценки обычно обозначать как а и b.

Тогда уравнение парной регрессии

у = а + bх (4.22)

есть оценка модели (4.21).

Уравнения (4.21) и (4.22) определяют прямую, пересекающую ось у (при х = 0) в точке а с тангенсом угла наклона b.

Уравнение (4.4.2) может быть преобразовано к виду:

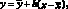(4.23)

где

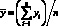; (4.24)

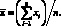(4.25)

В практических расчетах широко используют оба варианта уравнений – (4.22) и (4.23).

Вычисление коэффициентов а и b. Значения а и b вычисляют методом наименьших квадратов (м.н.к.) при соблюдении следующих допущений:

– значения х задаются (или измеряются) без погрешностей или их погрешности намного меньше погрешностей измерения значений у;

– регрессия линейна: у = а + bх;

– отклонения уi – Yi (разница между измеренным yi и вычисленным (оценочным) Yi значениями аналитического сигнала при x = xi) взаимно независимы и имеют одну и ту же дисперсию при всех х;

– отклонения (погрешности) распределены по нормальному закону (отклонения от нормального закона встречаются довольно часто, но они принимаются во внимание, если весьма значительны);

– отсутствуют посторонние переменные, существенно уменьшающие роль связи между х и у.

Аналитически задача м. н. к. выражается следующим образом:

Yl = a + bxl. (4.26)

Если обозначить уi – (а + bxi) = ?i, то

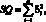i, …, n. (4.27)

Следовательно, задача линейного регрессионного анализа (м.н.к.) заключается в том, чтобы сумма квадратов отклонений экспериментальных точек (yi, xi) вдоль ординаты от проведенной прямой была минимальной.

Для того, чтобы найти параметры а и b, удовлетворяющие минимуму SQ, берут частные производные выражения (4.27) относительно а, затем относительно b; полученные выражения приравнивают нулю:

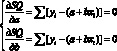(4.28)

находят систему нормальных уравнений и, решая ее, получают:

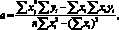(4.29)

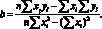(4.30)

В тех случаях, когда а мало отличается от нуля, необходима проверка его значимости. Для этого при расчетах на ЭВМ после расчета дисперсии оценки необходимо введение соответствующей подпрограммы.

Таблица 4.4

Методика вычисления коэффициентов регрессии

Вычисление коэффициентов регрессии удобно проводить в табличной форме (табл. 4.4)

Используя данные табл. 4.4, получаем:

у = ?yi/n;

Для проверки правильности вычислений в табл. 4.4 можно использовать выражение:

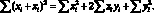(4.31)

Дисперсия оценки . Дисперсия оценки характеризует меру разброса (рассеяния) экспериментальных данных (xi, yi) относительно прямой. Ее вычисляют по формуле:

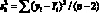(4.32)

при числе степеней свободы f = n – 2. Однако, если для каждой из проб проводят по ki параллельных измерений, так что имеется nki, = п? результатов измерений, то с формулой. (4.32) будет связано не f = п – 2, a f = п? – 2, которое и будет в знаменателе.

Положительное значение корня из называют стандартной ошибкой оценки. Обе эти величины – и s0 как правило, печатаются в выходных данных.

При расчетах на ЭВМ удобнее пользоваться формулой:

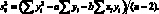(4.33)

Сумму квадратов в уравнении удобнее определять, пользуясь выражениями:

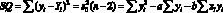(4.34)

или

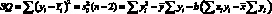. (4.35)

При вычислениях по формулам (4.32)–(4.35) все расчеты необходимо выполнять при достаточно большом числе знаков после запятой, так как сумму квадратов часто ищут для весьма близких значений. Поэтому на этом этапе даже незначительные погрешности в вычислении могут привести к большим погрешностям.

Дисперсии и стандартные отклонения коэффициентов а и b.

Коэффициенты а и b являются случайными величинами. Их расчет по формулам (4.36), (4.37) можно рассматривать как расчет результатов косвенных измерений. Ввиду этого необходима оценка доверительных интервалов констант а и b, которая выполняется на основании значений стандартного отклонения свободного члена sa и стандартного отклонения коэффициента регрессии sb.

Дисперсии и  коэффициентов а и b находят, пользуясь законом накопления (распространения) ошибок; стандартные отклонения sa и sb рассчитывают по формулам:

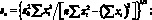(4.36)

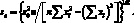(4.37)

со степенями свободы f = п – 2.

* Эквивалентные формулы:

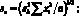(4.38)

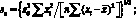(4.39)

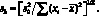(4.40)

Анализ формулы (4.40) показывает, что дисперсия коэффициента регрессии тем меньше, чем дальше значение хi лежит от его среднего значения х, т.е., чем шире интервал концентраций (содержаний), выбранный для построения градуировочной кривой.

Интервальные значения констант ?0 и ?. Интервальные значения констант ?0 и ?. [см. уравнение (4.21)] находят из формул:

(4.41)

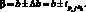(4.42)

при f = n – 2 или f = n’ – 2 (см. выше).

Зная ?а и ?b, определяют число необходимых знаков после запятой для значений а и b.

Коэффициент корреляции r. Для описания тесноты связи (корреляции) параметров х и у в линейном регрессионном анализе используют коэффициент корреляции r, выборочное значение которого вычисляют по формуле:

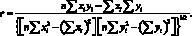(4.43)

Коэффициент корреляции может изменяться от 0 до 1. Чем ближе r к 1, тем ближе изучаемая зависимость к функциональной (не стохастической) зависимости между исследуемыми величинами, а r = 0 свидетельствует о полной взаимной независимости (отсутствии корреляционной связи) величин х и у.

Доверительные интервалы линии регрессии. Оценки а и b содержат погрешности (Sa, Sb). Вследствие этого значение аналитического сигнала Yi, вычисляемого по уравнению Yi = a + bxi, – необходимо рассматривать также как случайную величину, дисперсия которой () будет складываться из двух составляющих: и . В этом случае при заданном (стандартном, эталонном) значении х0 доверительный интервал вычисляемого значения Y0 (Y0 = а + bх0)[6] будет определяться формулой:

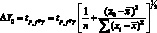(4.44)

или

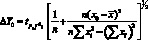(4.45)

при f = n – 2. При больших значениях n и ?(xi)2 выражение (4.44) аппроксимируется «быстрым» доверительным интервалом.

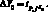
Если нанести на график интервальные значения Y0 ± ?Y0 (вычислены для разных заданных значений хо, взятых во всем рассматриваемом интервале xi), то они образуют доверительную зону.

Доверительная зона определяет местоположение линии регрессии, но не отдельных возможных значений зависимой переменной, которые отклоняются от нее.

Доверительный интервал единичных значений зависимой переменной Yp. Если определяют доверительные интервалы для отдельных (единичных) значений зависимой переменной, то при вычислении дисперсии 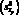необходимо дополнительно учитывать и дисперсию оценки 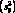(рассеяние вокруг линии регрессии). В этом случае доверительные интервалы для прогнозируемых индивидуальных значений Yp(Yp = a + bxo)[7] будут равны:

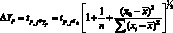(4.46)

или

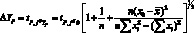
при f = п – 2, а интервальные значения переменной Yр ± ?Y0p.

Это – уравнение гиперболы относительно переменных х0 и Yо.