
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Дискретная оптимизация и моделирование в условиях неопределенности данных
Перепелица В. А., Тебуева Ф. Б.,
4.2.2. Клеточно-автоматное прогнозирование
Исходные данные, используемые в процессе реального математического моделирования, получаются, как правило, путем прогнозирования, в частности, прогнозирования ВР. Сложившаяся к настоящему времени (будем говорить «классическая») теория прогнозирования ВР в определенных случаях демонстрирует приемлемую точность прогнозирования (неточность получаемых прогнозов не превосходит погрешность измерения исходных статистических данных). Достаточно представительное изложение современных (классических) методов прогнозирования ВР можно найти в [90]. Эти методы не являются универсальными, т.к. используемые для их разработки подходы и инструментарий обосновывались в предположении, что для прогнозируемых ВР выполняется целый ряд специфических условий.
В обширном многообразии принципов и подходов к построению классических моделей прогнозирования, отметим тот набор понятий, которые являются базовыми: экстраполяция с помощью сглаживания (вычисление скользящей средней); авторегрессия (авторегрессионные скользящие средние вида ARMA и ARIMA [90]); допущение линейности относительно параметров и переменных; выделение детерминированных или стохастических трендов; использование регрессионных уравнений при условии, что исходные статистические данные позволяют отражать дисперсионно-ковариационные параметры и др. Реализуемые на этой базе методы не являются универсальными, т.к. используемые для их разработки подходы и инструментарий обосновывались в предположении, что для прогнозируемых ВР выполняется целый ряд специфических условий. Например, в многомерных обобщениях прогнозных ARMA-моделей используются байесовские авторегрессионные модели. В силу этого принципиально важным условием является предположение о том, что возмущения (т.е. положительные и отрицательные приращения уровней ВР) являются независимыми и, следовательно, подчиняются нормальному закону (белый шум). Это условие не выполняется для реальных ВР, имеющих долговременную память. Что касается вышеупомянутого условия линейности, то оно порождает (для многих практически полученных данных) проблему неадекватности ARMA-моделей. В контексте методологического анализа адекватности классических подходов к прогнозированию конкретных ВР, нужно (в дополнение к вышеуказанному) принимать во внимание и другие условия: учет или неучет (фильтр) флуктуаций (выбросов), что родственно наличию «тяжелых хвостов» [69], [73] или «джокера» [15]; возможности декомпозиционного анализа [41]; предположение о стохастическом (случайном) порождении уровней рассматриваемого ВР и соответствующее условие стационарности [90] этого ВР.
На наш взгляд, решение проблемы разработки методов прогнозирования ВР с памятью и нелинейностью следует искать в использовании методов нелинейной динамики, в первую очередь – в использовании инструментария клеточных автоматов [9], [47], [71]. Идею клеточно-автоматного прогнозирования, включая использование нечетких систем [13], [19], [39], [40], [76] мы продемонстрируем на примере ВР спроса населения на медицинские услуги [37]. Прогнозируемые значения этого спроса являются исходными данными для задачи целочисленного программирования в региональной операции управления запасами [37].
Основу информационного пространства при изучении спроса населения на медицинские услуги составляют временные ряды (ВР) посуточных обращений для получения медицинской помощи. Введем обозначения для трёх ВР ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() , где
, где ![]() – это ВР посуточных количеств заболеваний ОРЗ среди детей возрастной группы от 0 до 15 лет за период с 1993 по 2003 год,
– это ВР посуточных количеств заболеваний ОРЗ среди детей возрастной группы от 0 до 15 лет за период с 1993 по 2003 год, ![]() и
и ![]() – это результат агрегирования ВР
– это результат агрегирования ВР ![]() с интервалом агрегирования, равным одной неделе и одному месяцу соответственно.
с интервалом агрегирования, равным одной неделе и одному месяцу соответственно.
Для построения памяти прогнозной модели на базе линейного клеточного автомата [9], [34], [47], [71] исходный ВР, например ![]() , переводится в лингвистический временной ряд (ЛВР):
, переводится в лингвистический временной ряд (ЛВР): ![]() ,
, ![]() , элементы которого принимают значения из терм-множества
, элементы которого принимают значения из терм-множества ![]() , где
, где ![]() , означает низкий (средний, высокий) уровень заболеваемости,
, означает низкий (средний, высокий) уровень заболеваемости, ![]() ,
, ![]() . Комбинаторной базой построенной памяти клеточного автомата являются всевозможные
. Комбинаторной базой построенной памяти клеточного автомата являются всевозможные ![]() - конфигурации вида
- конфигурации вида ![]() ,
, ![]() ,
, ![]() , где
, где ![]() – глубина памяти [73] данного ЛВР (для полученного конкретного ЛВР
– глубина памяти [73] данного ЛВР (для полученного конкретного ЛВР ![]() значение
значение ![]() );
); ![]() – множество всех содержащихся в ЛВР
– множество всех содержащихся в ЛВР ![]()
![]() - конфигураций, которые пронумерованы индексом
- конфигураций, которые пронумерованы индексом ![]() ,
, ![]() . Каждая
. Каждая ![]() - конфигурация
- конфигурация ![]() имеет определенное число
имеет определенное число ![]() её вхождений в данный ЛВР
её вхождений в данный ЛВР ![]() и определенное число
и определенное число ![]() переходов в “событие”
переходов в “событие” ![]() ,
, ![]() определяющие собой частость этих переходов
определяющие собой частость этих переходов 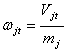 . Память клеточного автомата – массив данных
. Память клеточного автомата – массив данных ![]() ,
, ![]() ,
, ![]() .
.
Если в данном ЛВР имеет место переход всякого вхождения конкретной конфигурации ![]() в одно и то же событие
в одно и то же событие ![]() , то говорим, что
, то говорим, что ![]() представляет собой «конфигурацию с памятью». Для ЛВР
представляет собой «конфигурацию с памятью». Для ЛВР ![]() с глубиной памяти
с глубиной памяти ![]() вычислительная схема предлагаемого алгоритма прогнозирования значения элемента
вычислительная схема предлагаемого алгоритма прогнозирования значения элемента ![]() состоит из последовательного построения «деревьев переходов» такого вида, как показано на рис.4.8. В терминах теории графов процесс построения такого дерева исчерпывается тогда, когда все его «висячие вершины» представляют собой конфигурации с памятью. Каждая вершина – конфигурация в дереве переходов взвешена соответствующим значением частости переходов. На базе этих частостей формируется первое прогнозное значение элемента
состоит из последовательного построения «деревьев переходов» такого вида, как показано на рис.4.8. В терминах теории графов процесс построения такого дерева исчерпывается тогда, когда все его «висячие вершины» представляют собой конфигурации с памятью. Каждая вершина – конфигурация в дереве переходов взвешена соответствующим значением частости переходов. На базе этих частостей формируется первое прогнозное значение элемента ![]() в виде лингвистического нечеткого множества (ЛНМ)
в виде лингвистического нечеткого множества (ЛНМ) ![]() ,
, ![]() Второе прогнозное значение получается путем преобразования ЛНМ
Второе прогнозное значение получается путем преобразования ЛНМ ![]() в числовое, т.е. обычное нечеткое множество (НМ)
в числовое, т.е. обычное нечеткое множество (НМ) ![]() ,
, ![]() . Числовые значения
. Числовые значения ![]() этого НМ получаются путем замены в ЛНМ лингвистических термов
этого НМ получаются путем замены в ЛНМ лингвистических термов ![]() на подходящие числовые значения, выбранные из исходного ВР
на подходящие числовые значения, выбранные из исходного ВР ![]() . Завершающей операцией прогнозирования является операция дефазификации [99], с помощью которой прогнозное НМ
. Завершающей операцией прогнозирования является операция дефазификации [99], с помощью которой прогнозное НМ ![]() преобразуется в обычное числовое значение
преобразуется в обычное числовое значение ![]() .
.
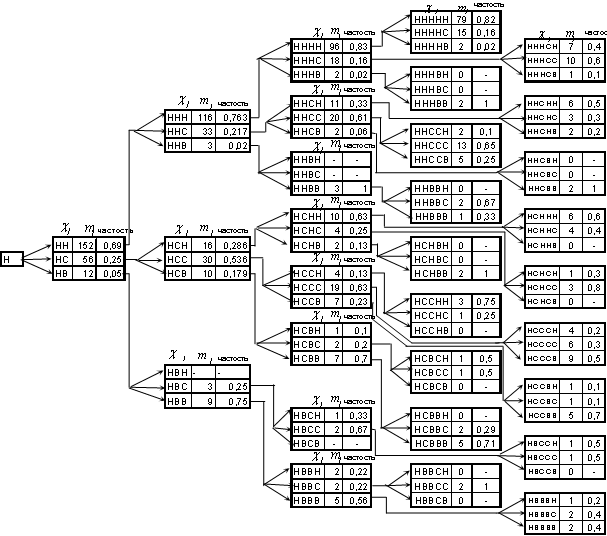
Рисунок 4.9. Геометрическое представление переходов всех начинающихся с терма «Н»
![]() -конфигураций лингвистического временного ряда
-конфигураций лингвистического временного ряда ![]() для
для ![]()
Основная цель агрегирования исходного подневного ВР ![]() в еженедельный ВР
в еженедельный ВР ![]() и в помесячный ВР
и в помесячный ВР ![]() состоит в том, чтобы получить возможность наряду с краткосрочным (подневным) прогнозированием осуществлять среднесрочное (понедельное) и долгосрочное (помесячное) прогнозирование. Вместе с тем следует отметить, что операция агрегирования может приводить как к уменьшению погрешности прогнозирования, так и к увеличению этой погрешности. Так, результаты ретропрогноза для еженедельного ВР
состоит в том, чтобы получить возможность наряду с краткосрочным (подневным) прогнозированием осуществлять среднесрочное (понедельное) и долгосрочное (помесячное) прогнозирование. Вместе с тем следует отметить, что операция агрегирования может приводить как к уменьшению погрешности прогнозирования, так и к увеличению этой погрешности. Так, результаты ретропрогноза для еженедельного ВР ![]() значительно превосходят в положительную сторону результаты ретропрогноза для ежемесячного ВР
значительно превосходят в положительную сторону результаты ретропрогноза для ежемесячного ВР ![]() . На основании валидации получены оценки средней погрешности прогноза для ВР
. На основании валидации получены оценки средней погрешности прогноза для ВР ![]()
![]() и для ВР
и для ВР ![]()
![]() соответственно.
соответственно.