Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

МЕТОДЫ ФОТОМЕТРИЧЕСКОГО АНАЛИЗА В САНИТАРНО-ГИГИЕНИЧЕСКИХ ИССЛЕДОВАНИЯХ

Дорогова В Б, Игнатьева Л П,

4.3. Оценка правильности результатов измерений (определений)

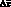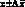После того как осуществлена проверка грубых погрешностей (в случае подозрительных результатов измерений) и их исключение, производят оценку доверительного интервала (36.wmf) для среднего значения 266.wmf, интервальных значений 37.wmf и при необходимости – оценку правильности результатов.

Доверительный интервал (Ах). Если воспроизводимость результатов измерений (методики анализа) характеризуют стандартным отклонением, то сами результаты измерений (определений) характеризуют доверительным интервалом среднего значения 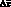36.wmf, который рассчитывают по формуле:

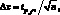38.wmf (4.13)

Здесь tр,f – квантиль распределения Стьюдента при числе степеней свободы f = n – 1 и двухсторонней доверительной вероятности P (значения см. tр,f в табл. 4.3).

Доверительный интервал может быть задан как абсолютной погрешностью с представлением в тех единицах, в которых выражается результат анализа, так и относительной погрешностью, выраженной в процентах от результата анализа: 100?x/x [ %(отн.)] или 100?x/?, [ % (отн.)] (при наличии стандартных или эталонных образцов).

Обычно для расчетов доверительного интервала пользуются значениями Р = 0,95; иногда достаточно Р = 0,90, но при ответственных измерениях требуется более высокая надежность (Р = 0,99).

Необходимо отметить, что, если при отработке методики выполняют n параллельных определений, а методика анализа в дальнейшем предусматривает выдачу результатов из m параллельных определений (обычно n ? 10, m = 2:3), то доверительный интервал для рядовых анализов следует рассчитывать по 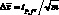39.wmf, a не по 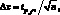38.wmf (где s – стандартное отклонение для выборки из n опытов). В противном случае значение 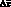36.wmf рядового анализа окажется слишком заниженным.

Коэффициент tP,f показывает, во сколько раз разность между истинным и средним результатами больше стандартного отклонения среднего результата:

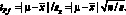40.wmf (4.14)

Интервальные значения измеряемой величины. В общем случае интервальные значения измеряемой величины при выбранной доверительной вероятности определяются выражениями:

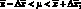41.wmf (4.15)

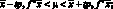42.wmf (4.16)

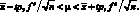43.wmf (4.17)

Таблица 4.3

Значения квантилей t-распределения в зависимости от доверительной вероятности Р (двусторонняя постановка задачи) и 33.wmf (односторонняя постановка задачи) и степени свободы

f

Р

0,75

0,90

0,95

0,98

0,99

33.wmf

0,875

0,95

0,975

0,99

0,995

1

2,41

6,31

12,7

31,82

63,7

2

1,60

2,92

4,30

6,97

9,92

3

1,42

2,35

3,18

4,54

5,84

4

1,34

2,13

2,78

3,75

4,60

5

1,30

2,01

2,57

3,37

4;03

6

1,87

1,94

2,45

3,14

3,71

7

1,25

1,89

2,36

3,00

3;50

8

1,24

1,86

2,31

2,90

3,36

9

1,23

1,83

2,26

2,82

3,25

10

1,22

1,81

2,23

2,76

3,17

11

1,21

1,80

2,20

2,72

3,11

12

1,21

1,78

2,18

2,68

3,05

13

1,20

1,77

2,16

2,65

3,01

14

1,20

1,76

2,14

2,62

2,98

15

1,20

1,75

2,13

2,60

2,95

16

1,19

1,75

2,12

2,58

2,92

17

1,19

1,74

2,11

2,57

2,90

18

1,19

1,73

210

2,55;

2,88

19

1,19

1,73

2,09

2,54

2,86

20

1,18

1,73

2,09

2,53

2,85

21

1,18

1,72

2,08

2,52

2,83

f

Р

0,75

0,90

0,75

0,98

0,75

33.wmf

0,875

0,95

0,875

0,99

0,875

22

1,18

1,72

2,07

2,51

2,82

23

1,18

1.7L

2,07

2,50

2,81

24

1,18

1,71

2,06

2,49

2,80

25

1,18

1,71

2,06

2,49

2,79

26

1,18

1,71

2,06

2,48

2,78

28

1,17

1,70

2,05

2,47

2,76

30

1,17

1,70

2,04

2,46

2,75

?

1,15

1,64

1,96

2,33

2,58

Доверительный интервал ограничивает область, внутри которой при отсутствии систематических погрешностей находится истинное значение измеряемой величины [см. формулу (4.15)] с заранее заданной доверительной вероятностью Р.

Из формул (4.13) и (4.17) следует, что доверительный интервал зависит от размера выборки, т.е: от числа проведенных опытов: с уменьшением числа измерений п увеличивается доверительный интервал (при той же доверительной вероятности) или при заданном доверительном интервале уменьшается надежность измерений[4].

Пользуясь соотношениями (4.13) и (4.15) и данными табл. 4.3 можно рассчитывать доверительные интервалы при выбранных значениях Р или, наоборот, задавшись определенным доверительным интервалом, можно рассчитать t,f и по табл. 4.3 оценить его доверительную вероятность.

Значимость систематической погрешности. О значимости систематической погрешности, т.е. о правильности результата анализа, судят в зависимости от того, попадает ли истинное значение определяемой величины в установленный доверительный интервал или находится вне его. Если 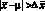44.wmf, то можно говорить о значимой систематической погрешности Е, интервальное значение которой заключено в пределах:

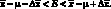45.wmf (4.18)

В этом случае необходимо выяснить причину появления систематической погрешности

Правильность результатов определений можно контролировать различными способами и, в первую очередь, путем сопоставления следующих величин:

а) результата анализа стандартного образца (СО), полученного по применяемой методике, с паспортными данными СО;

б) введенного и найденного содержания добавки стандартного раствора определяемого элемента к анализируемому раствору;

в) результатов анализа одного и того же образца данного вещества, полученных в разных лабораториях;

г) результатов анализа одного и того же образца данного вещества при помощи методики, используемой для контроля продукции, и арбитражной методики анализа.

При сопоставлении величин по пп. «а–г» правильность результатов аналитических определений считают удовлетворительной, если выполняется одно из следующих неравенств:

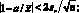46.wmf (4.19)

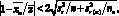47.wmf (4.20)

где а –

аттестованное значение содержания определяемого компонента в стандартном образце или известное содержание добавки согласно п. «б»;

266.wmf –

среднее арифметическое результатов п параллельных определений при анализе образца по пп. «а – г» в лаборатории;

48.wmf –

среднее арифметическое результатов па параллельных определений при анализе образца по п. «б» в арбитражной лаборатории или при помощи арбитражной методики анализа;

sr(a) –

относительное стандартное отклонение единичного результата, полученное в арбитражной лаборатории или для арбитражной методики анализа.

В отсутствие стандартных образцов правильность результатов определений может быть оценена путем постановки специальных опытов по «схеме удвоения» в сочетании с методом добавок.

Для обнаружения и исключения систематических погрешностей широко применяют также регрессионный и корреляционный анализы.

Для полной характеристики методики на правильность необходима оценка систематических погрешностей вблизи нижней и верхней границ интервала Сn – Св.