Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Дискретная оптимизация и моделирование в условиях неопределенности данных

Перепелица В. А., Тебуева Ф. Б.,

3.1. Введение к главе

Известными классическими экстремальными задачами на графах являются, например, задача о раскраске вершин графа и задача об определении чисел внешней и внутренней устойчивости [17], [45], [50]. В настоящей книге мы практически не будем касаться этих и других задач, являющихся традиционными для теории графов. Объектом нашего внимания являются такие формулируемые на языке теории графов задачи, которые по своей сущности и по своему происхождению скорее относятся к задачам математического программирования. Общая особенность этих задач состоит в том, что они формулируются на взвешенных графах.

В зависимости от содержательной интерпретации заданные веса ребер этих графов отражают значения таких показателей, как урожайность сельскохозяйственных культур [67], заболеваемость населения [71], ожидаемое количество застрахованных лиц [70], объемы вредных выбросов [61] и т.д. Значения этих показателей принципиально не могут представляться действительными числами, наоборот, их прогнозируемые значения могут оказаться интервалами [11], нечеткими множествами [76], включая лингвистические термы [13] и т.д. С учетом этого обстоятельства представляемые в настоящей книге алгоритмы дискретной оптимизации [80], [88] исполняют роль «базовых элементов» в следующем смысле:

· в условиях вышеотмеченной неопределенности исходных данных  каждый из этих алгоритмов является лишь вычислительной схемой, для которой остается нерешенной проблема реализации на ПЭВМ вычислительного процесса с нечеткими, интервальными и т.п. данными;

· в смысле прикладных аспектов они могут исполнять роль «алгоритмов с оценками» [25], если нечеткие значения заменить определенными числами, например, средними;

· в методологическом отношении представленные ниже доказательства могут исполнять роль аналогий в процессе реализации строгого обоснования алгоритмов, применяемых к экстремальным комбинаторным задачам с нечеткими данными.

В самом общем виде математическую постановку экстремальной задачи на графах можно описать следующим образом. Задается - вершинный граф , чаще всего со взвешенными элементами. Заданием графа неконструктивно определяется множество или система  некоторых объектов. Часто s – это некоторая часть графа . Например, s – это совершенное паросочетание, или гамильтонов путь, или покрытие и т.д. Задается также целевая функция , определенная на элементах множества . Задача состоит в том, чтобы в множестве  выделить элемент , который является экстремальным согласно целевой функции  (на элементе  функция  принимает значение  или ). Как правило, мощность множества очень велика по сравнению с числом вершин графа . Например, если  – множество гамильтоновых путей в полном ориентированном графе , то мощность . Вследствие этого решать поставленную задачу методом перебора всех элементов из  не представляется возможным. Поэтому в более точной формулировке смысл экстремальной задачи на графе состоит в том, чтобы построить достаточно эффективный алгоритм, который гарантированно находит оптимум в случае, если множество допустимых решений  не пусто.

Пусть  – это число вершин в графе . Алгоритм можно считать достаточно эффективным, если он находит точное решение задачи и при этом затрачивает порядка  операций, где  – константа. Под операцией понимаем сравнение двух чисел или арифметическую операцию. Теоретический интерес представляют и такие алгоритмы трудоемкости , для которых справедливо соотношение .

Ниже мы приведем математическую постановку и примеры содержательного  смысла нескольких известных экстремальных задач на графах. В дальнейшем через  будем обозначать - вершинный неориентированный (ориентированный) граф с множеством ребер (дуг)  и множеством вершин , перенумерованных индексом . Если граф  является взвешенным, то через  обозначается вес ребра (дуги) .

Если экстремальная задача сформулирована на взвешенном графе , то её множество допустимых решений (МДР) обозначаем через , где  – это удовлетворяющий соответствующим условиям подграф графа , , . Качество допустимых решений  определяется целевой функцией (ЦФ) , которая достаточно часто имеет вид (3.1), т.е. представляет собой суммарный вес ребер подмножества :

 , .(3.1)

1. Задача о кратчайшей связывающей сети (ЗКСС): на неориентированном - вершинном графе с взвешенными ребрами требуется выделить  ребер так, чтобы выделенные ребра образовали связную сеть (точнее, остовное дерево) и при этом сумма весов ребер сети, т.е. значение целевой функции вида (3.1) было бы минимальным.

2.  Задача коммивояжера означает задачу нахождения простого -вершинного цикла (контура) минимального веса. К этой задаче сводится задача нахождения гамильтоновой цепи (гамильтонова контура) с ЦФ вида (3.1). Последняя возникает на практике, например, в случае процесса моделирования переналадок прокатного стана.

Первую постановку задачи коммивояжера осуществил H. Whitney в 1934 г., до настоящего времени эта задача не решена в том смысле, что для неё неизвестен достаточно эффективный алгоритм, в том числе и для случая, когда нужно найти хотя бы одно допустимое решение, т.е. выделить в данном графе  гамильтонов цикл (контур) .

3.   Задача об Эйлеровом обходе (оптимальный маршрут обхода ребер графа). В данном -вершинном связном взвешенном графе  рассматриваем множество маршрутов обхода всех ребер . Это множество содержит и такие маршруты, которые через некоторые ребра проходят многократно. Иллюстративный пример на рис.3.1 демонстрирует Эйлеров маршрут, который имеет 2-кратное прохождение по ребрам  и . С учетом этой кратности определяется длина маршрута, т.е. при вычислении этой длины вес ребра умножается на кратность его прохождения. Требуется найти маршрут минимальной длины. Эта задача сводится к известной полиномиальной задаче нахождения оптимального совершенного паросочетания в полном взвешенном графе размерности  и, следовательно [65], для неё существуют достаточно эффективные алгоритмы.

В качестве примера практического использования задачи об Эйлеровом обходе можно назвать моделирование процесса геофизической разведки на нефть и газ, когда требуется указать маршрут обхода сети «профилей» санным поездом [46].

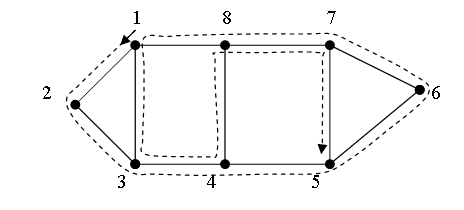
Рисунок 3.1. Маршрут обхода всех ребер 8-вершинного графа; 2-кратный проход по ребрам (3, 4) и =(7, 8)

4. Задача о кратчайшей цепи (кратчайшем пути). На графе  выделена пара вершин , . Требуется найти цепь (путь) , ,  из  в  такой, чтобы сумма (3.1) весов ребер (дуг), составляющих эту цепь (этот путь), была минимальной.

Задача решена в том смысле, что для нее существует эффективный алгоритм при условии неотрицательных весов ребер (дуг):  . Для этой задачи неизвестен эффективный метод решения, если она формируется при дополнительном условии: требуется найти цепь (путь), которая (который) включает в себя заранее выделенные вершины исходного графа . Указанный особый случай – это задача, родственная задаче коммивояжера.

5. Задача о критическом пути. В силу специфики практического применения эта задача обычно формулируется только на ориентированном графе с одним входом  и одним выходом . Входом называют вершину, из которой дуги только исходят, выходом называют вершину, в которую инцидентные ей дуги только входят. Критическим называют такой путь  из  в , для которого сумма весов его дуг вида (3.1) является максимальной. В сетевом графике на рис.3.2 критический путь выделен жирными дугами.

Содержательная постановка задачи о критическом пути возникает обычно при реализации комплекса работ, взаимный порядок выполнения которых обусловлен технологией и задается в виде ориентированного графа без контуров. В этом графе дугам приписаны продолжительности соответствующих работ. При отсутствии дефицита на ресурсы критический путь определяет минимально возможную продолжительность выполнения всего комплекса работ. В иллюстративном примере на рис.3.2 критический путь  и его вес . Задача о критическом пути состоит в нахождении этого пути и вычислении его веса.

Для решения однокритериальной, т.е. оптимизационной задачи о критическом пути существует достаточно эффективные алгоритмы [98]. В условиях многокритериальности [74], когда качество решения оценивается определенной на X векторной целевой функцией , , , , оптимальные допустимые решения, вообще говоря, отсутствуют. В этом случае возникает необходимость находить паретовское множество  [74], т.е. множество паретооптимальных допустимых решений, в силу чего экстремальная задача на графах становится труднорешаемой [30].

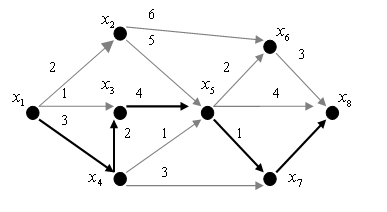
Рисунок 3.2. Сетевой график и критический путь на нем

6. Задача о покрытии графа ребрами [5]. Для заданного -вершинного неориентированного графа  без изолированных вершин требуется найти такое множество ребер , чтобы выполнялись следующие два условия:

1) каждая вершина исходного графа была инцидентна хотя бы одному ребру из ;

2) мощность  множества  минимальна.

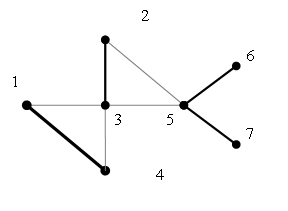
Рисунок 3.3. Пример допустимого покрытия 7-вершинного графа

Удовлетворяющее этим условиям подмножество  называется допустимым покрытием, которое можно называть допустимым решением этой задачи и обозначать через , где всякая вершина  инцидентна хотя бы одному ребру из .

В иллюстративном примере на рис.3.3 множество жирных ребер является допустимым покрытием и, вместе с тем, является минимальным покрытием.

7. Взвешенная задача о покрытии [65]. Сформулированную в предыдущем п.6 задачу можно рассматривать на взвешенном графе, определяя аналогичным образом множество допустимых решений (покрытий) . На  определена целевая функция вида (3.1).

Сформулированная выше задача о покрытии является частным случаем «задачи покрытия графа типовыми подграфами», в которой допустимое решение представляет собой такой остовный подграф  данного графа , ребру , , в котором каждая компонента связности изоморфна некоторому типовому графу из заданного множества типовых графов. Эти задачи о покрытии имеют важные приложения в теории синтеза схем, производственной психологии, землепользовании и других областях. К настоящему времени эффективных методов решения этих задач еще не найдено.

8. Задача о совершенном паросочетании является следующим особым случаем задачи о покрытии -вершинного графа ребрами:  – чётно и задача состоит в том, чтобы найти покрытие, состоящее из  ребер. Для этой задачи известны достаточно эффективные методы её решения, например, полиномиальный алгоритм, описанный в работе [65], трудоемкость которого составляет  операций.

9. Задача об оптимальном паросочетании состоит в нахождении такого совершенного паросочетания на n-взвешенном графе, у которого сумма весов ребер, составляющих это паросочетание, достигает экстремума согласно (3.1). Вычислительная сложность этой задачи ограничена сверху оценкой [65].

10. Задача о китайском почтальоне. Задан неориентриванный граф со взвешенными ребрами. Требуется найти такой замкнутый маршрут обхода всех вершин этого графа, в котором длина пройденного пути (т.е. суммарный вес ребер) была бы наикратчайшей. При этом разрешается многократное прохождение одного и того же ребра, например, в изображенном на рис.3.4 маршруте ребро  проходится дважды. В целевой функции вида (3.1) веса ребер суммируются с учетом кратности их происхождения. Эта задача также решена в смысле существования полиномиального алгоритма.

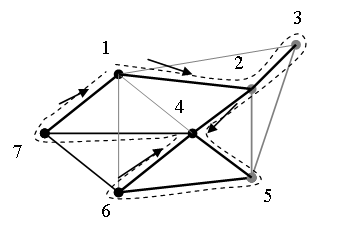
Рисунок 3.4

11. Задача  коммивояжеров представляет собой такую постановку сформулированной в п.7 задачи покрытия взвешенного графа типовыми графами, когда последние являются элементарными циклами (контурами) число вершин которых удовлетворяет заданным ограничениям. Целевая функция имеет вид (3.1). При  получаем обычную (классическую) задачу коммивояжера (см. п.2).

Задача  коммивояжеров имеет важное приложение в календарном планировании. Укажем конкретный пример. Пусть имеется  станков или автоматических линий, для которых заказ (т.е. календарная производственная программа) состоит из  партий изделий. Пусть  – длительность изготовления -й партии, а  – время, затрачиваемое на переналадку его с обработки -й партии на обработку -й партии. Возникает следующая задача календарного планирования: так распределить  партий по  линиям и запуск распределенных на каждую линию партий, чтобы длительность выполнения всего заказа была наикратчайшей.

Задача  коммивояжеров является существенно сложнее классической «задачи коммивояжера». Здесь требуется осуществить не только оптимальное упорядочение, но и наилучшее распределение партий по линиям.