Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Дискретная оптимизация и моделирование в условиях неопределенности данных

Перепелица В. А., Тебуева Ф. Б.,

2.3.4. Оптимизация при диофантовых соотношениях

Диофантовым уравнением называется полиномиальное уравнение с целыми коэффициентами, которое требуется решить в целых (часто положительных) числах.

Примечание 2.2. Уравнение с рациональными коэффициентами эквивалентно уравнению с целыми коэффициентами. Например, уравнение  можно переписать в виде .

Решение линейного диофантова уравнения

тесно связано с задачей отыскания числа всевозможных способов разбиения целого  на слагаемые, принадлежащие множеству целых положительных чисел .

Часто диофантово уравнение или система таких уравнений ,  определяют множество ограничений в задачах оптимизации. Решение таких задач методом полного перебора всех разбиений не представляется возможным в силу необозримости возможных вариантов.

10-я проблема Гильберта (1901).Найти алгоритм, при помощи которого можно после конечного числа операций определить, имеет ли данное диофантово уравнение целочисленное решение.

Ю.В. Матиясевич доказал (70 лет спустя), что требуемого (для сформулированной проблемы) алгоритма в природе не существует.

Вернемся к нашей задаче о делении линии и сформулируем ее следующим образом. Выбрать положительные целые числа , , которые максимизируют сумму

 (2.16)

при ограничении

 (2.17)

Обозначим через  оптимум задачи (2.16)-(2.17) и представим величину  в виде , где  – натуральное и .

Теорема 2.1. Если требуется найти  и целые числа , , представляющие оптимальное решение задачи о делении линии, то искомый оптимум имеет следующий вид:

 и

, , при ;

; , , при

; , при .

Доказательство.Сначала заметим, что в оптимальном решении  заведомо  для всех . Далее, если , то его можно записать . Наконец, если , то  можно заменить на и , произведение которых . Следовательно, в оптимальном решении все  равны 2 или 3. Кроме того, сумма  сомножителей  равно сумме  сомножителей , откуда получаем, что если произведение (1.16) содержит , то последнее можно заменить на . Таким образом, если – оптимум, то произведение (2.15) имеет вид

, где  (2.18)

Оставшаяся часть доказательства теоремы 2.1 непосредственно следует из (2.18) и рассмотрения трех случаев: , и .

Рассмотрим задачу максимизации произведения

 (2.19)

при диофантовом ограничении

 (2.20)

Здесь – положительное целое число, а значение  – не фиксировано.

Теорема 2.2.Положительные целые числа максимизируют при ограничении (2.20) тогда и только тогда, когда , , т.е. оптимальное решение задачи (1.19)-(1.20) имеет вид , .

Доказательство.Пусть оптимальное решение задачи (2.19)-(2.20) представляет собой вектор .

Предположим противное, т.е. допустим, что вектор  содержит компоненту . Рассмотрим сначала случай, когда . Таким образом, произведение (2.19) содержит множитель . Поскольку  не фиксировано, то можем заменить на два сомножителя . Значит для всякого  значение .

Пусть теперь . Тогда  можем заменить на , где , а .

Полученное противоречие и доказывает теорему 2.2.

Сформулируем теперь без доказательства теорему, устанавливающую конкретно вид оптимального решения задачи (2.19)-(2.20).

Теорема 2.3.Если , и  – количество единиц, двоек и троек в решении, данном теоремой 2.2, то максимум целевой функции (2.19) достигается в точках целочисленной решетки, определяемых системой неравенств:

;

;

;

.

Рассмотрим задачу, в некотором смысле обратную рассмотренной выше задаче о делении линии. Требуется найти натуральные , , максимизирующие сумму

 (2.21)

при ограничении

 (2.22)

Сформулируем очевидное

Утверждение 2.4. Пусть . Тогда оптимальное решение задачи (2.21)-(2.22) имеет вид: , а для остальных  значения . Такой же вид будет иметь решение в случае, если целевая функция (2.21) будет иметь вид:

 ,  .

Рассмотрим теперь класс задач, в котором допустимые решения определяются диофантовым ограничением вида

 (2.23)

где – заданное натуральное число. Требуется найти вектор с целочисленными неотрицательными компонентами , доставляющий минимум (максимум) целевой функции следующего вида

 (2.24)

где – выпуклые (вогнутые) функции от одного переменного. Малотрудоемкий алгоритм решения задачи (2.23)-(2.24) можно построить благодаря следующему установленному О. Гроссом критерию:

Теорема 2.4.Пусть ,  – выпуклые функции одного переменного. Необходимое и достаточное условие того, что вектор с неотрицательными целочисленными компонентами  минимизирует выражение (2.24) при ограничении (2.23) состоит в том, что является справедливым соотношение , где множество индексов , .

Ниже мы сформулируем и докажем утверждение, частным случаем которого является теорема 2.4. А сейчас опишем принцип работы алгоритма для задачи (2.23)-(2.24).

Решение этой задачи в случае выпуклых  получается за  шагов, которые будем нумеровать числами . Вектор промежуточного решения, получаемого на -ом шаге, обозначим через .

Результатом первого шага считаем нулевой вектор . Пусть в результате -го шага получен вектор  и пусть – такое значение индекса , что выполняется равенство  .

Тогда на -ом шаге полагаем: , а для всех остальных принимаем . Образно выражаясь, можно сказать, что искомое решение получается путем распределения  единиц среди  возможных значений , причем на каждом шаге одна единица придается аргументу той функции , которая имеет наименьшее приращение.

Если все функции  одинаковы, то искомое оптимальное решение получается сразу, а именно, из теоремы 2.4 вытекает

Следствие 2.1.Пусть в задаче (2.23)-(2.24) все функции  одинаковы, т.е.  для всех , где  – выпуклая или вогнутая функция. Тогда оптимальное решение имеет вид:

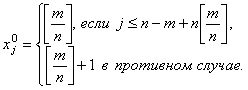
Приведем содержательную и математическую формулировку одной конкретной экстремальной комбинаторной задачи, которая может послужить иллюстративным примером для общей постановки (2.23)-(2.24).

Пусть  – это число единиц данного оружия, которое предназначается для уничтожения  вражеских целей. Введем следующие обозначения: – количество единиц этого оружия, выделенных для поражения -ой цели, которой приписана стоимость , ; – вероятность поражения -й цели при использовании единицы данного оружия. Если , то вероятность выживания -й цели после обстрела ее  единицами оружия равна . Задача заключается в максимизации ожидаемой стоимости пораженных целей или в минимизации стоимости сохранившихся целей. После представления целевой функции вида (2.24) это означает, что требуется найти вектор с целочисленными компонентами , который минимизирует сумму , при ограничениях , , , ,  – действительные числа.