Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Дискретная оптимизация и моделирование в условиях неопределенности данных

Перепелица В. А., Тебуева Ф. Б.,

2.3.1. Вложение дискретной задачи в непрерывную и использование методов математического анализа

П.Л. Чебышев: “Математика создалась и развивалась под влиянием общей и основной задачи всей человеческой деятельности: распорядиться имеющимися под руками средствами для достижения наибольшей выгоды”.

Начнем с примера.Проектируется строительство нового микрорайона (или нового города в неосвоенных районах) с населением  человек. Требуемое число продовольственных магазинов для этого микрорайона обозначим через . Строительство каждого магазина обходится в единиц. Суммарные затраты самого населения микрорайона (потери времени на посещение магазина, простои в очередях и т.п.) выражаются величиной . Требуется найти такое число магазинов , при котором суммарные затраты на обслуживание района, выражаемые (для определенности) целевой функцией

 (2.8)

были бы наименьшими.

Решение. Пусть  фиксировано: . Целевая функция задана на дискретном множестве . Попытаемся расширить ее на большее не дискретное пространство – на множество вещественных положительных чисел. При этом заметим, что  есть сумма двух величин:  и , каждая из которых является выпуклой функцией от . Подразумевается, что  пробегает все вещественные значения положительной полуоси абсцисс (см. рис.2.3).

Рисунок 2.3

 Исследуя графики ,  и , убеждаемся, что сумма  также выпуклая функция от . Поэтому, естественным образом, напрашивается способ нахождения оптимального значения  рассматриваемой задачи методами математического анализа, что не представляет труда. Сначала находим корень уравнения  В нашем случае это корень находим из уравнения: , .

Искомый оптимум

 (2.9)

т.е. для нахождения  достаточно вычислить значение целевой функции в двух ближайших к целочисленных точках оси абсцисс.

Справедливость (2.9) следует из выпуклости функционала (2.8): .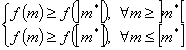 Тогда функцию  можно представить себе, как непрерывную функцию от : , где ,  и .

Функция , очевидно, является непрерывной выпуклой и дифференцируемой по . Решая уравнение , находим на положительной оси абсцисс точку , в которой  достигает минимума. Условимся здесь и в дальнейшем обозначать:

 – наибольшее целое, не превосходящее числа ,

 – наименьшее целое, которое не меньше числа .

В силу выпуклости  искомое целочисленное значение , при котором  достигает минимума, находится из соотношения:

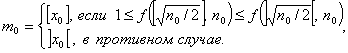
Но мы ищем определенную формулу , которая представляла бы оптимальное целочисленное значение  для всякого натурального , а не только для фиксированного .

Ведь может случиться, что при одном значении для нашей задачи о магазинах искомый оптимум , а при другом значении  искомый оптимум . Поэтому задача будет считаться решенной только после того, как мы покажем справедливость одного из двух неравенств:

1)  при всех ,

2)  при всех .

Для нашей задачи о магазинах нетрудно показать, что при всех выполняется первое из указанных неравенств. Действительно неравенство 1) означает, что для всех

 (2.10)

Это неравенство равносильно соотношению

,

которое после упрощений имеет вид

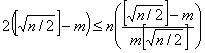
или

  или  (2.11)

 Очевидно, неравенство (2.11), а вместе с ним и (2.10), справедливо для всякого .

Аналогично показывается, что при  также выполняется (2.10). Таким образом, для всякого натурального  искомый оптимум требуемого числа магазинов находится по формуле .

Описанная выше дискретная задача с минимизируемой целевой функцией (2.8) свелась к поиску минимума выпуклой функции  от одной переменной. При этом для отыскания целочисленного оптимума нам пришлось сравнить значения этой функции всего лишь в двух точках:  и . Рассмотрим теперь случай, когда дискретную целевую функцию задачи можно расширить до непрерывной выпуклой функции , заданной в - мерном пространстве .

Из классической теории оптимизации известно, что найти точку , , в которой  достигает минимума, не представляет особого труда в случае выпуклости . Однако, нас интересует не сама точка , координаты , которой, скорее всего, не являются целыми числами. В поиске искомого решения, нужно рассматривать точки целочисленной решетки, которые окружают . Следовательно, если  – дробные числа для всех , то нам нужно просмотреть значений, которые функция  принимает в точках целочисленной решетки, соседних с . Например, если в некоторая выпуклая функция  достигает минимума с целочисленными координатами, то нам нужно просмотреть  значения: , ,  и .

Величина очень быстро растет с ростом . Например, при  вычислить значения  в  точках решетки и выбрать среди них минимум не под силу ни одной из современных ПЭВМ, т.к. это требует сотни лет непрерывного счета. Таким образом, даже если критерий эффективности представляет собой выпуклую (т.е. «хорошую» в классическом смысле) функцию, то поиск целочисленного оптимума в общем случае может представлять собой непреодолимые вычислительные трудности. В этом и заключается так называемое «проклятие размерности».

Замечание 2.1. Функция называется выпуклой, если для всякого числа и всякой пары точек  выполняется неравенство

 (2.12)

где . Функция называется вогнутой, если в определении (2.12) знак  заменить на знак . На рис.2.3 приведен пример выпуклых функций, при этом отметим, что линейная функция  является одновременно и вогнутой функцией от m. Поиск целочисленного максимума фактически идентичен поиску минимума выпуклой функции.

Замечание 2.2.Прием, который мы назвали «вложением дискретной задачи в непрерывную», иногда полезен не только в случаях выпуклой или вогнутой функций . Очень часто удается быстро отыскать интересующий нас экстремум для монотонной, унимодальной и других видов целевой функции. Естественно, что и этим случаям присущи проблемы, связанные с перебором целочисленных узлов, окружающих экстремальную точку непрерывного графика.