
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Дискретная оптимизация и моделирование в условиях неопределенности данных
Перепелица В. А., Тебуева Ф. Б.,
2.2. Верхняя, нижняя и точная оценки оптимума Функция Шеннона
Использование понятий «максимум» или «минимум» данной величины является для нас привычным делом и, как правило, в смысловом плане не вызывает затруднений. Трудности здесь возникают в том случае, если становится необходимым представить эти величины в аналитическом виде. Приведем несколько элементарных теорем, которые могут оказаться полезными в дальнейшем.
Утверждение 2.1.
![]() (2.1)
(2.1)
Полезно привести доказательство утверждения (2.1), поскольку оно является типичным рассуждением при обосновании такого рода соотношений. Доказательство очень короткое и состоит в следующем. Если ![]() , то
, то ![]() и
и ![]() , откуда следует искомый результат, т.к.
, откуда следует искомый результат, т.к. ![]() является максимумом. Если же
является максимумом. Если же![]() , то
, то ![]() является максимумом. Действительно, в этом случае
является максимумом. Действительно, в этом случае ![]() и, таким образом, правая часть (2.1) равна
и, таким образом, правая часть (2.1) равна ![]() , что и требовалось доказать.
, что и требовалось доказать.
Утверждение 2.2.
![]() (2.2)
(2.2)
Доказательство:
![]() , и, применяя предыдущий результат, получаем
, и, применяя предыдущий результат, получаем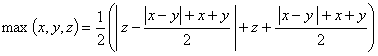 , откуда и следует искомый результат.
, откуда и следует искомый результат.
Утверждение 2.3.
![]() (2.3)
(2.3)
Соотношения (2.1)-(2.3) – это примеры аналитического представления значений экстремумов в простейших случаях. Их число можно было бы приумножить, но они не представляют самостоятельного значения и чаще всего используются в промежуточных выкладках при обосновании различных соотношений. В теории комбинаторных экстремальных задач существуют экстремальные величины, которые имеют более сложную природу и которые представляют самостоятельный научный интерес. Одну из таких величин – функцию Шеннона мы рассмотрим на примере одной календарной задачи. Сначала приведем содержательное описание задачи, а затем ее математическую постановку.
Пусть требуется выполнить ![]() работ. Каждая работа состоит из
работ. Каждая работа состоит из ![]() различных операций, одних и тех же для всех работ и выполняемых в определенном порядке, вообще говоря, разном для разных работ. Одновременно две (и более) одинаковые операции выполняться не могут. Длительность выполнения всех операций одинакова и равна 1. Обозначим совокупность из
различных операций, одних и тех же для всех работ и выполняемых в определенном порядке, вообще говоря, разном для разных работ. Одновременно две (и более) одинаковые операции выполняться не могут. Длительность выполнения всех операций одинакова и равна 1. Обозначим совокупность из ![]() указанного вида работ через
указанного вида работ через ![]() . Требуется составить кратчайшее расписание выполнения данных работ. Длительность такого кратчайшего расписания обозначим через
. Требуется составить кратчайшее расписание выполнения данных работ. Длительность такого кратчайшего расписания обозначим через ![]() .
.
Иногда вместо «работ» и «операций» говорят о составлении оптимального расписания для обработки ![]() деталей, каждая из которых проходит обработку на
деталей, каждая из которых проходит обработку на ![]() станках. Порядок прохождения по станкам для каждой детали свой.
станках. Порядок прохождения по станкам для каждой детали свой.
Основная (и до сих пор нерешенная) задача здесь – это обоснование достаточно эффективного алгоритма, который бы строил оптимальное (т.е. кратчайшее) расписание для всякого ![]() , где
, где ![]() – множество всех возможных совокупностей из
– множество всех возможных совокупностей из ![]() работ. Наряду с этим большой теоретический интерес представляет нахождение аналитического выражения функции Шеннона, которая определяется как функция
работ. Наряду с этим большой теоретический интерес представляет нахождение аналитического выражения функции Шеннона, которая определяется как функция ![]() от размерности задачи
от размерности задачи ![]() ,
, ![]() :
:
![]() (2.4)
(2.4)
Содержательно величину (2.4) можно трактовать как формулу, по которой можно вычислить значение «наихудшего» оптимума при фиксированной размерности задачи.
Прежде чем обсуждать проблему нахождения функции Шеннона, приведём математическую постановку нашей задачи. Занумеруем все работы из ![]() числами
числами ![]() , а все виды операций числами
, а все виды операций числами ![]() . Тогда множество
. Тогда множество ![]() можно представить в виде исходной матрицы
можно представить в виде исходной матрицы ![]() размерности
размерности ![]() , где
, где ![]() число, обозначающее операцию, которая стоит на
число, обозначающее операцию, которая стоит на ![]() -м месте в
-м месте в ![]() -ой работе. Иными словами каждая
-ой работе. Иными словами каждая ![]() -я строка матрицы
-я строка матрицы ![]() – это некоторая перестановка
– это некоторая перестановка ![]() , в котором на
, в котором на ![]() -м месте стоит номер той операции которой должна подвергнуться
-м месте стоит номер той операции которой должна подвергнуться ![]() -я работа после того, как пройдет предписанные ей первые
-я работа после того, как пройдет предписанные ей первые ![]() операции.
операции.
Таблица 2.1
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 3 | 5 | 7 | 8 | 2 | 4 | 6 | 9 |
| 1 | 4 | 6 | 7 | 9 | 2 | 5 | 8 | 3 |
В таблице 2.1 приведен пример исходной матрицы ![]() , которая полностью характеризует множество из трёх работ, состоящих из 9 операций каждая.
, которая полностью характеризует множество из трёх работ, состоящих из 9 операций каждая.
Определим теперь понятие расписания ![]() , где
, где ![]() – это матрица размерности
– это матрица размерности ![]() ,
, ![]() , элементами
, элементами ![]() которой являются натуральные числа
которой являются натуральные числа ![]() , а также нули или прочерки (пустые клетки). В этом расписании ненулевой элемент
, а также нули или прочерки (пустые клетки). В этом расписании ненулевой элемент ![]() обозначает номер операции, которая должна выполняться для
обозначает номер операции, которая должна выполняться для ![]() -й работы в течение отрезка времени
-й работы в течение отрезка времени ![]() . Если
. Если![]() , то это означает, что на отрезке времени
, то это означает, что на отрезке времени ![]() никакая операция для
никакая операция для ![]() -й работы не выполняется. Матрица
-й работы не выполняется. Матрица ![]() называется допустимым расписанием для исходной матрицы
называется допустимым расписанием для исходной матрицы![]() , если она удовлетворяет следующим условиям:
, если она удовлетворяет следующим условиям:
1)каждая строка ![]() ,
, ![]() , матрицы
, матрицы ![]() содержит по одному ненулевому элементу
содержит по одному ненулевому элементу ![]() , взаимный порядок расположения которых (в строке) совпадает с порядком расположения этих элементов в
, взаимный порядок расположения которых (в строке) совпадает с порядком расположения этих элементов в ![]() -й строке матрицы
-й строке матрицы ![]() ;
;
2)в каждом столбце матрицы ![]() все ненулевые элементы попарно различны;
все ненулевые элементы попарно различны;
3)матрица ![]() является не уплотняемой в том смысле, что при попытке переместить какой либо ненулевой элемент
является не уплотняемой в том смысле, что при попытке переместить какой либо ненулевой элемент ![]() на один столбец влево мы нарушим условие 2).
на один столбец влево мы нарушим условие 2).
Таблица 2.2
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|
|
|
|
|
|
|
|
| 1 | - | 3 | - | 5 | - | 7 | - | 9 | 2 | 4 | 6 | 8 |
|
|
|
|
| 1 | - | 4 | - | 6 | - | 7 | - | 9 | 2 | 5 | - | 8 | 3 |
Таблица 2.2 представляет одно из допустимых расписаний для исходной матрицы ![]() , представленной в таблице 2.1. Нетрудно проверить, что представленное таблицей 2.2 расписание, удовлетворяет всем трем условиям из определения допустимого расписания.
, представленной в таблице 2.1. Нетрудно проверить, что представленное таблицей 2.2 расписание, удовлетворяет всем трем условиям из определения допустимого расписания.
Число столбцов ![]() матрицы
матрицы ![]() есть длительность этого расписания. В дальнейшем число
есть длительность этого расписания. В дальнейшем число ![]() будем называть длиной расписания
будем называть длиной расписания ![]() . Если
. Если ![]() является оптимальным (т.е. кратчайшим) расписанием для
является оптимальным (т.е. кратчайшим) расписанием для ![]() , то число столбцов матрицы
, то число столбцов матрицы ![]() будем обозначать через
будем обозначать через ![]() . Ясно, что
. Ясно, что ![]() есть функция от
есть функция от ![]() :
: ![]()
![]() (2.5)
(2.5)
где максимум берется по всевозможным ![]() матрицам S, представляющим совокупности работ
матрицам S, представляющим совокупности работ ![]() .
.
Поскольку в сформулированной нами задаче календарного планирования длительность выполнения всех операций одинакова, то можно считать, что величина (2.5) отражает как бы влияние различного порядка выполнения операций на длину оптимального расписания.
Как мы уже заметили, до сих пор остается нерешенной основная задача построения достаточно эффективного алгоритма, который бы для всякой исходной матрицы ![]() находит кратчайшее расписание
находит кратчайшее расписание ![]() . Но наряду с этим весьма трудной оказывается и задача обоснования аналитического выражения величины (2.5). К настоящему времени функция Шеннона (2.5) известна только для случая двух работ:
. Но наряду с этим весьма трудной оказывается и задача обоснования аналитического выражения величины (2.5). К настоящему времени функция Шеннона (2.5) известна только для случая двух работ: ![]() , где
, где ![]() – целая часть числа
– целая часть числа ![]() .
.
Нерешенная задача:найти точное значение функции Шеннона для случая трех работ, т.е. найти формулу для ![]() .
.
Понятие функции Шеннона используется в самых различных задачах и, как правило, обосновать эту величину очень трудно. Поэтому в теории экстремальных комбинаторных задач значительный интерес представляет нахождение «хороших» верхних и нижних оценок функции Шеннона, которые для рассматриваемой иллюстративной задачи обозначим соответственно через ![]() и
и ![]() . Этот вопрос очень тесно связан с поиском приближенных решений оптимизационных задач. Что касается величины (2.5), то для нее известны следующие нижняя и верхняя оценки:
. Этот вопрос очень тесно связан с поиском приближенных решений оптимизационных задач. Что касается величины (2.5), то для нее известны следующие нижняя и верхняя оценки:
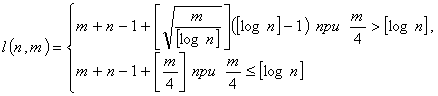 (2.6)
(2.6)
и
![]() (2.7)
(2.7)
Заметим, что является справедливым неравенство ![]() , т.е. нижняя оценка (2.6) ограничена сверху величиной, линейно зависящей от
, т.е. нижняя оценка (2.6) ограничена сверху величиной, линейно зависящей от ![]() и
и ![]() . В то же время верхняя оценка (2.7) является нелинейной функцией от
. В то же время верхняя оценка (2.7) является нелинейной функцией от ![]() и
и ![]() . Т.о., приведенные верхняя и нижняя оценки – это величины разного порядка, т.е., это «плохие» оценки, которые мало что нам говорят о характере функции
. Т.о., приведенные верхняя и нижняя оценки – это величины разного порядка, т.е., это «плохие» оценки, которые мало что нам говорят о характере функции ![]() .
.
Нерешенная задача: для случая, когда![]() ,
, ![]() – константа, требуется найти такую нижнюю оценку
– константа, требуется найти такую нижнюю оценку ![]() и такую верхнюю оценку
и такую верхнюю оценку ![]() , для которых отношение
, для которых отношение ![]() было бы ограничено сверху некоторой константой.
было бы ограничено сверху некоторой константой.
Гипотеза. Существует такая константа ![]() , что
, что![]() .
.
Если верхняя оценка равна нижней оценке, то говорят, что получена точная оценка.