Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Дискретная оптимизация и моделирование в условиях неопределенности данных

Перепелица В. А., Тебуева Ф. Б.,

1.2. Элементарные комбинаторные задачи

Несмотря на свою простоту и наглядность, комбинаторные задачи очень трудны, многие из них остаются нерешенными сотни лет. Например, определение числа магических квадратов порядка  при  является нерешенной к настоящему времени задачей.

Особое значение комбинаторика приобретает в XVI– XVIIIвв. в связи с возникновением теории вероятностей. Подсчет значений вероятности наступления того или иного события невозможен без комбинаторных операций.

До середины двадцатого столетия комбинаторные задачи чаще всего формулировались в наглядном развлекательном виде.

Рассмотрим, например, выпущенную в свет в 1908 году книгу Е.И. Игнатьева «В царстве смекалки» [36]. В ней содержится более 200 задач, среди которых преобладают комбинаторные или с элементами комбинаторики. Приведем некоторые из них.

Задача 9.Положено 5 спичек (см. рис.1.1). Прибавьте к ним еще 5 спичек, чтобы получилось три.

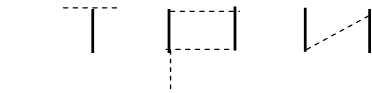
Рисунок 1.1

 Задача 21.Спички расположены, как показано на рис.1.2. Переложить две спички так, чтобы получилось 5 равных квадратов.

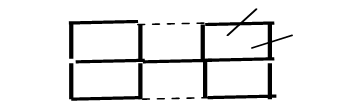
Рисунок 1.2

 Задача 23.В фигуре, изображенной на рис.1.3, переложить 5 спичек так, чтобы всего получилось 2 квадрата.

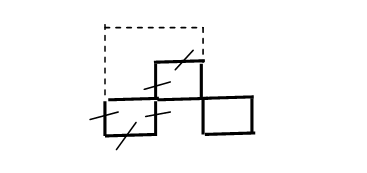
Рисунок 1.3

 Покажем, как геометрические задачи-игры со спичками могут послужить основой для серьезного теоретико-числового результата.

Задача 42. Рассмотрим таблицу

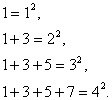
Доказать, что сумма первых  нечетных чисел, может быть равной квадрату их числа.

Возьмем квадрат из  клеток и для заштрихуем клетки так, как это сделано на рис.1.4.

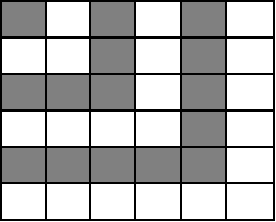
Рисунок 1.4

 Чередующиеся светлые и темные участки позволяют увидеть, что количество клеток в них, начиная с левого верхнего угла возрастает на 2 на каждом переходе: 1, 3, 5, 7, 9 и т.д. Следовательно, число клеток в квадрате  равно , что и требовалось доказать.

Комбинаторными являются и многие задачи с дробями.

Задача 52.Можно ли разделить поровну 5 пряников между шестью мальчиками, не разрезая ни одного пряника на 6 равных частей?

Ответ:Можно, сначала 3 пряника разрежем пополам и половинки раздадим. Оставшиеся 2 пряника разрежем каждый на 3 равные части и равные доли раздадим. Всем поровну и ни одного пряника не пришлось разрезать на 6 частей.

Задача 11.Записать единицу используя три цифры пять с какими угодно знаками математических действий.

Ответ:.

Аналогично:

Задача 119.Записать 2 тремя «5»: .

Задача 120.Записать 4 тремя «5»: .

Задача 121.Записать 5 тремя «5»: .

Задача 122.Записать 0 тремя «5»: .

Задача 123.Записать 31 пятью «3»:

.

Комбинаторным задачам присущ тот «интригующий момент», который неизменно вызывает у пытливой личности повышенный интерес и возбуждает желание попробовать свои силы в решении их. Для своего решения эти задачи требуют проявить догадку, математическое остроумие и некоторое умственное напряжение. В процессе их решения развиваются комбинаторные способности и математическое воображение.

В подтверждение сказанного приведем серию задач комбинаторного характера из пособия для учителей П.Ю. Германовича «Сборник задач по математике на сообразительность».

№2. Два отца и два сына пошли погулять и купили 3 апельсина. Каждому из них досталось по одному апельсину. Как это могло случиться?

№6. Рассмотрим 9-ти этажный дом. Во сколько раз лестница на 9-й этаж длиннее лестницы на 2-й этаж?

№33. На берегу реки стоят трое взрослых и два мальчика. У них есть лодка, вмещающая лишь одного взрослого или двух мальчиков. Как всем пятерым переправиться на другой берег?

№37. Может ли сумма двух чисел равняться их разности? (Ответ: да – , если ).

№42. Сумма и произведение четырех целых чисел равны 8. Что это за числа? (Ответ: 1, 1, 2, 4).

№44. Мальчик хочет 30 орехов разложить на 3 кучки так, чтобы число орехов в каждой кучке было нечетным. Какой совет вы дали бы мальчику? (Ответ: невозможно разложить).

Относительно серии этих задач можно сделать следующие 2 замечания:

1. Процесс решения комбинаторных задач не подчиняется какому-либо общему решению. Каждая оригинальная комбинаторная задача требует для решения особого подхода, т.е. процесс ее решения сродни искусству. Л. Толстой отмечал: «Наука и искусство так же тесно связаны, как легкие и сердце…».
2. Великие деятели искусства, литературы в прошлом и настоящем неоднократно обращались к математике. Изречение А.С. Пушкина: «Вдохновение нужно в геометрии, как и в поэзии»; изречение М.В. Ломоносова «А математику уже учить следует за то, что она ум в порядок приводит».

Приведем задачу, которую придумал Л.Н. Толстой: «Косцы должны скосить 2 луга. С утра они все вместе стали косить большой луг. По происшествие половины рабочего дня косцы разделились: половина их осталась на большом лугу и к вечеру его докосили, а другая половина перешла косить другой луг, вдвое меньший первого, но не успела к концу дня закончить косьбу. На другой день на этот луг вышел один косец и в течение всего дня докосил его. Сколько всего было косцов?»

Примечание 1.1. В решении приведенной выше задачи фигурируют дроби, однако это чисто комбинаторная задача.

Приведем комбинаторные задачи геометрического типа.

1. Существуют ли треугольники, у которых один из углов равен разности двух других углов? (Ответ: да – все прямоугольные треугольники).
2. Можно ли разносторонний треугольник разрезать на два равных треугольника? (Ответ: нет – резать необходимо через вершину).
3. Можно ли утверждать, что любая вписанная в круг трапеция равнобедренная? (Ответ: можно, т.к. дуги между параллельными хордами равны, значит и стороны, стягивающие хорды также равны).
4. Квадрат и ромб имеют равные периметры. Площадь какой фигуры больше? (Ответ: квадрата).

Приведем более простую комбинаторную задачу, которую можно отнести к категории задач средней сложности.

№47. Имеется 10 одинаковых по размеру и виду кубиков. Одни из них алюминиевые (более легкие), другие – дюралевые (потяжелее). Определить число кубиков каждого вида с помощью не более шести взвешиваний на чашечных весах.

Рассмотрим алгоритм, сложность которого характеризуется значением .

Сначала составим план решения. Будем стремиться составить пару из алюминиевого и дюралевого кубиков, чтобы сравнивать вес этой пары с весом любой другой пары, тогда результат каждого взвешивания сразу дает подсчет тех и других кубиков в испытываемой паре.

Первое ветвление от корня дерева (дуги (1) и (2) на рис.1.5) соответствуют следующим рассуждениям.

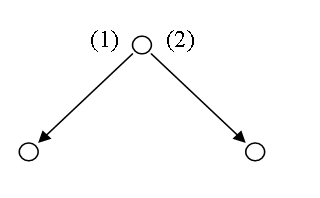
Рисунок 1.5

 Положим на чашки весов по кубику.

1. Если равновесия нет, то кубики разнородны и пара из двух разнородных кубиков получена. Сравнивая вес ее с весом каждой из четырех оставшихся пар, мы с помощью пяти взвешиваний подсчитаем число кубиков каждого рода.
2. Если же было равновесие, то кубики первой пары однородны. Тогда на одну чашку весов положим эту пару, а на другую чашку – вторую пару (второе взвешивание). Допустим, опять наступило равновесие. Значит, все 4 кубика одного рода, но какого, пока неизвестно.

Заменим вторую пару новой третьей парой (третье взвешивание). Допустим, что третья пара перетянула. Значит испытанные 4 кубика алюминиевые, а в новой паре либо оба кубика дюралевые, либо один дюралевый, другой алюминиевый.

Состав этой 3-й пары выясним на 4-ом взвешивании: ее кубики положим на разные чашки весов. В случае равновесия оба кубика дюралевые и т.д. В первых трех парах – 4 алюминиевых и 2 дюралевых. Если нет равновесия – 5 алюминиевых и 1 дюралевый.

Здесь в обоих случаях уже можем составить пару из разнородных кубиков и с ее помощью на 5-ом и 6-ом взвешивании выяснить состав оставшихся 4-х кубиков.

Приведем чисто старинную комбинаторную задачу, которую придумал Ньютон и сформулировал в виде стихотворения. В переводе на русский язык она звучит так: «Мне нужна Ваша помощь, чтобы посадить девять деревьев в десять рядов так, чтобы в каждом ряду было три дерева. Скажи – как, и я ничего больше не спрошу». (Решение задачи приведено на рис.1.6).

Рисунок 1.6