
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
2.2.1. Задача о волновом сопротивлении СВП при нестационарном режиме движения в битых льдах
Известно, что при движении СВП по чистой воде или по полю битого льда образуется гравитационная волна, идущая в направлении движения судна. Если СВП движется в непосредственной близости от кромки сплошного льда, то данная волна при определенных условиях может разрушать ледяной покров. Чем больше крутизна и амплитуда волны, тем больше вероятность разрушения ледяного покрова, находящегося в непосредственной близости от движущегося судна. Основной характеристикой, отвечающей за амплитуду и крутизну волны, является волновое сопротивление судна. Волновое сопротивление, в свою очередь, зависит от параметров льда, водоема, характеристик судна и скорости движения. Скорость движения может быть постоянной, но чаще в реальных условиях скорость движения зависит от времени. Чаще всего на практике судно начинает движение с ускорения, затем выходит на стационар и после этого тормозит до полной остановки. Ранее в работе [63] рассматривалось равноускоренное и стационарное движение СВП в битых льдах.
В данной главе рассматривается случай, когда СВП движется на различных нестационарных режимах. Рассматривается бесконечная область, покрытая битым льдом, по которой со скоростью u(t) перемещается заданная система поверхностных давлений q(x,y,t). Совмещенная с судном система координат располагается следующим образом: плоскость xOy совпадает с невозмущенной поверхностью раздела лед-вода, ось x направлена в сторону движения судна, ось z – вертикально вверх. Предполагается, что вода - идеальная несжимаемая жидкость плотностью r2, движение жидкости потенциальное. Поверхностная плотность флотирующей жидкости задается непрерывной функцией m(x,y) [124, 31]:
![]() .
.
где r1(x,y) – «размазанная» по поверхности жидкости плотность льда; r10 – физическая плотность льда; s1(x,y) – безразмерная функция сплоченности льда (0 ≤ s1 ≤ 1); h(x,y) – толщина льда. В дальнейшем предполагается, что r1 и h – величины постоянные.
Согласно [17,109] величина волнового сопротивления, действующего на СВП, вычисляется по формуле
 (2.36)
(2.36)
где W - область распределения нагрузки q(x,y,t); w(x,y,t) – деформация поверхности флотирующей жидкости, определяемая в линейной теории волн в заданной системе координат следующим образом [63]:
 (2.37)
(2.37)
Здесь u – скорость системы поверхностных давлений q, ![]() - функция потенциала скоростей жидкости.
- функция потенциала скоростей жидкости.
Искомая функция потенциала скорости![]() должна удовлетворять уравнению Лапласа
должна удовлетворять уравнению Лапласа ![]() и линеаризованным граничным условиям [63]
и линеаризованным граничным условиям [63]
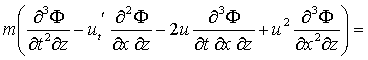
 (2.38)
(2.38)
где ![]() H1 –глубина водоема,
H1 –глубина водоема, ![]() - глубина погружения льда при статическом равновесии. Для больших глубин, когда H1 намного больше h, можно считать
- глубина погружения льда при статическом равновесии. Для больших глубин, когда H1 намного больше h, можно считать ![]() .
.
При условии, что в момент времени t=0 судно не имеет хода и отсутствуют любые возмущения, кроме статической деформации свободной поверхности, начальные условия для функции![]() запишутся в виде [63]:
запишутся в виде [63]:
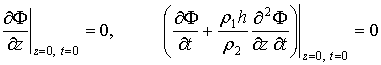 (2.39)
(2.39)
Предполагается, что закон изменения скорости движения судна (системы поверхностных давлений) в зависимости от времени можно приближенно выразить следующей формулой:
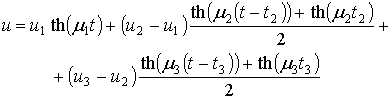 (2.40)
(2.40)
где u1, u2, u3 – значения скоростей, на которые последовательно выходит судно; m1, m2 и m3 – коэффициенты, отвечающие за ускорение (торможение) судна, значения t2 и t3 соответствуют временам, при которых ускорение судна равно![]() и
и ![]() соответственно, и являются также точками перегиба графика функции u(t) (см. рис.2.25).
соответственно, и являются также точками перегиба графика функции u(t) (см. рис.2.25).
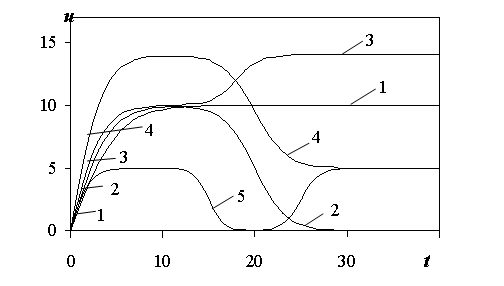
На рис. 2.25 изображены режимы скорости судна (2.40) в зависимости от времени. Здесь кривая 1 соответствует первому типу движения (разгон – движение с заданной скоростью). Кривая 2 соответствует второму типу движения (разгон – движение с заданной скоростью – торможение до нуля). Кривая 3 третьему типу движения (разгон – движение с первой заданной скоростью – разгон – движение со второй заданной скоростью). Кривая 4 соответствует четвертому типу движения (разгон – движение с первой заданной скоростью – торможение – движение со второй заданной скоростью). Кривая 5 соответствует пятому типу движения (разгон – движение с заданной скоростью – торможение до нуля - разгон – движение с заданной скоростью).
 .
.
Рис. 2.25. Режимы скорости судна в зависимости от времени:
1 - u1= u2= u3= 10 м/c, ![]() ;
;
2 - u1=10 м/с, u2= u3=0 м/с, m1=0,25, m2=0,3, t2=20c;
3 - u1=10 м/с, u2= u3 =14 м/с, m1=0,3, m2=0,4, t2=18с;
4 - u1=14 м/с, u2= u3= 5 м/с, m1=0,3, m2=0,3, t2=20с;
5 - u1=5 м/с, u2=0 м/с, u3=5 м/с, m1=0,5, m2=0,6, m3=0,5, t2=15с, t3=25с.
В соответствии с (2.40) расстояние, пройденное судном, вычисляется по формуле
 (2.41)
(2.41)
В качестве системы перемещающихся давлений q(x,y) используется функция [139, 63]:
 (2.42)
(2.42)
где q0 – номинальное давление; L – длина судна; w=L/B – удлинение судна; B – ширина судна; a1, a2 – параметры, характеризующие степень отклонения распределения давления в продольном и поперечном направлениях от прямоугольной формы. Чем больше a1, a2 по величине, тем ближе форма распределения давления к прямоугольной. При a1, a2 ® q эквивалентно q0, равномерно распределенному по прямоугольнику. Для лучшего согласования теоретических результатов с экспериментом в работе [139] предложено использовать значения a1L=a2L=10.
Задача решается аналитически с использованием преобразований Фурье и Лапласа аналогично работе [63].
Для аналитического решения задачи совершается переход к безразмерной постановке. Для этого вводятся в качестве характерных размеров L - длина судна и u0 – характерная скорость, в качестве которой в дальнейшем выбирается скорость u1. Вводятся безразмерные переменные, функции и параметры:
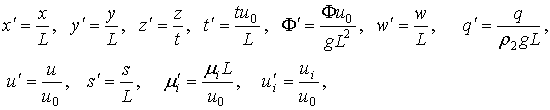 .
.
(штрихи в дальнейшем будем опускать). Тогда безразмерное граничное условие (2.38) для z=0 будет иметь вид:
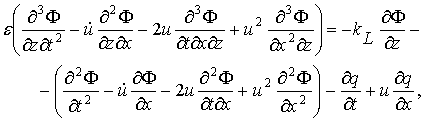 (2.43)
(2.43)
где kL=gL/u02, ε=ρ1h/ρ2L .
Предполагается, что функции Ф(x,y,z,t) и q(x,y) удовлетворяют условиям, необходимым для представления их в виде разложения в интеграла Фурье по двум переменным x и у:
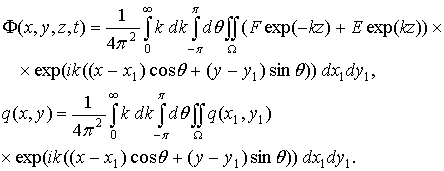 (2.44)
(2.44)
где F и E - неизвестные функции переменных x1, y1, t, k, θ. Подстановка выражений (2.44) в граничное условие (2.43) и обезразмеренное граничное условие (2.38) для ![]() , где
, где![]() =H/L позволяет получить зависимость между величинами F и E:
=H/L позволяет получить зависимость между величинами F и E:

![]()
![]()
![]() (2.45)
(2.45)
Тогда Ф(x,y,z,t) перепишется как:
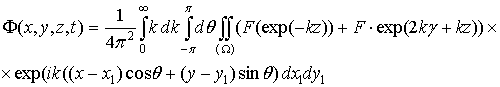
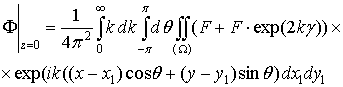
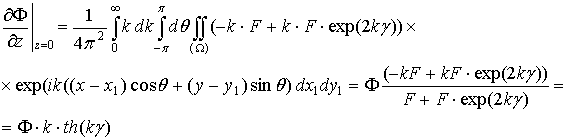 .
.
Здесь и далее подразумевается, что множители при Ф являются подынтегральными выражениями.
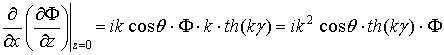

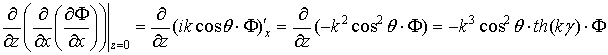 ,
,
 ,
,
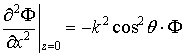 ,
,
 ,
,
 ,
,
![]() ,
,
Подставляя полученные выражения в (2.43), получим следующее уравнение:

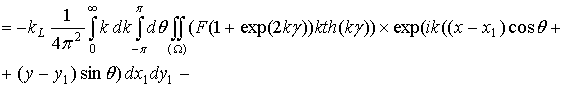

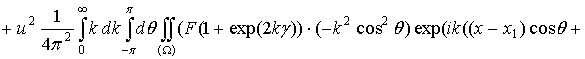
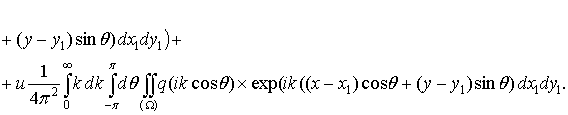 .
.
Опуская интегралы, получим следующее выражение для подынтегральных функций:
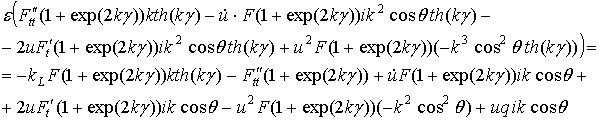 .
.
Разделив уравнение на![]() и сделав замену
и сделав замену ![]() , получим:
, получим:
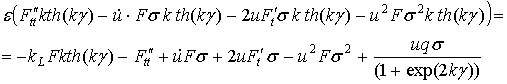 .
.
Приведем подобные члены:
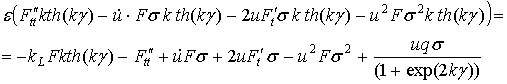 .
.
Разделим уравнение на![]() и получим дифференциальное уравнение для F:
и получим дифференциальное уравнение для F:
 (2.46)
(2.46)
где σ = ik cosθ.
Для решения (2.46) вводится в рассмотрение функция
![]() (2.47)
(2.47)
где – безразмерное расстояние, пройденное СВП за время t.
– безразмерное расстояние, пройденное СВП за время t.
Подстановка (2.47) в (2.46) дает следующие результаты:
![]() ,
,
![]() ,
,
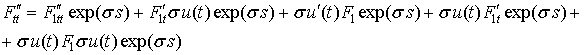 .
.
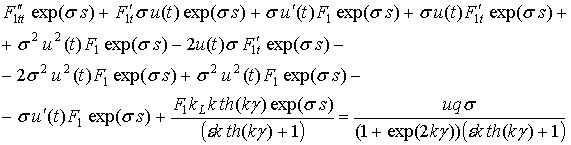 .
.
Приведя подобные члены, получим:
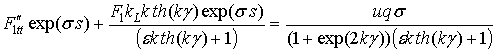 .
.
Домножим полученное выражение на ![]() :
:
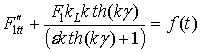 ,
,
где f(t)=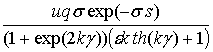 .
.
Используя преобразование Лапласа и начальные условия (2.39), имеем следующее уравнение для изображений функций F1 и f(t):
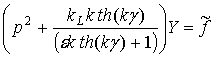 ,
, ![]() и
и ![]()
 ,
,
где 
Используя таблицу преобразований Лапласа, найдем оригинал для  :
:
 .
.
Пользуясь теоремой о свертке, получим следующее выражение для F1:
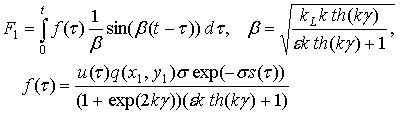 (2.48)
(2.48)
Подстановка (2.45) и (2.47) в (2.44) дает следующее выражение для функции Ф:
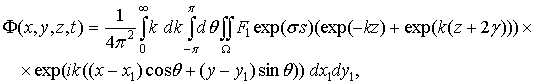 (2.49)
(2.49)
где F1 – вычисляется по (2.48).
Для нахождения волнового сопротивления R по формуле (2.36) необходимо переписать уравнение (2.37) в безразмерном виде.
 (2.50)
(2.50)
После подстановки (2.49), (2.50), (2.42) в (2.36) после несложных преобразований получится следующая интегральная формула для расчета волнового сопротивления СВП:
![]() ,
,![]() .
.
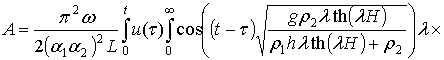 (2.51)
(2.51)

где u(t) вычисляется по обезразмеренной формуле (2.40), s(t) и s(t) – по обезразмеренной формуле (2.41).
Численные расчеты по формуле (2.51) проводились для a1L=a2L=10, r10=900 кг/м3, r2=1000 кг/м3, w=2, e - параметр флотации, ![]() .
.
На рис.2.26а показано изменение волнового сопротивления судна в зависимости от времени для H=3 м, L=10 м. Здесь кривые 1-5 для битого льда соответствуют режимам скоростей, представленным на рис.2.26б кривыми с соответствующими номерами. Пунктирные кривые 6-8 на рис.2.26а для чистой воды соответствуют режимам скоростей, представленным на рис. 2.26б кривыми 1-3. Из анализа рисунков 2.26а – 2.26б видно, что волновое сопротивление судна сильно зависит от того, до какой скорости разгоняется судно. Обычно скорости, при которых судно имеет максимальное волновое сопротивление, называют критическими. На рис. 2.26а кривые 1 и 6 соответствуют волновому сопротивлению при выходе судна через первый режим на докритическую скорость, кривые 2 и 7 – на околокритическую, кривые 3 и 8 – на сверхкритическую. Видно, что максимального волнового сопротивления судно достигает при движении с критической скоростью, при этом битый лед для докритических скоростей приводит к росту, а при критических и сверхкритических скоростях – к некоторому уменьшению волнового сопротивления при выходе на стационар. Данный вывод согласуется с результатами работы [65] для стационарного движения СВП. Кроме того, все кривые 1-3, 6-8 выходят с течением времени на свои стационарные значения [65,139] волнового сопротивления и в дальнейшем почти не меняются, сохраняя некоторый волнообразный характер. Кривая 4 рис. 2.26а показывает, что при торможении судна до нулевой скорости, волновое сопротивление несколько раз меняет свой знак и волнообразно стремится к нулю. Данный характер изменения волнового сопротивления, по-видимому, объясняется тем, что при торможении гидродинамическая волна опережает судно. При этом СВП сначала опускается на подошву волны, затем оказывается на той стороне волны, где величина ![]() , затем судно оказывается уже на гребне следующей волны, которая шла за ним, и т.д. И после того, как все гидродинамические волны обгонят судно, его волновое сопротивление выходит на нулевое значение. Анализ поведения кривых 3 и 5 рис. 2.26а показывает, что чем больше начальное ускорение (кривая 3), тем меньше основной горб волнового сопротивления при выходе на сверхкритическую скорость через первый режим движения. Заметим, что начальное ускорение при первом типе движения равно
, затем судно оказывается уже на гребне следующей волны, которая шла за ним, и т.д. И после того, как все гидродинамические волны обгонят судно, его волновое сопротивление выходит на нулевое значение. Анализ поведения кривых 3 и 5 рис. 2.26а показывает, что чем больше начальное ускорение (кривая 3), тем меньше основной горб волнового сопротивления при выходе на сверхкритическую скорость через первый режим движения. Заметим, что начальное ускорение при первом типе движения равно ![]() . Таким образом, для того, чтобы выйти на заданную сверхкритическую скорость с наименьшим волновым сопротивлением, СВП необходимо разгоняться до этой скорости с максимальным ускорением.
. Таким образом, для того, чтобы выйти на заданную сверхкритическую скорость с наименьшим волновым сопротивлением, СВП необходимо разгоняться до этой скорости с максимальным ускорением.
 .
.
Рис.2.26. Волновое сопротивление (а) при H=3 м, L=10 м, и скорость судна (б)в зависимости от времени: 1 - u1= u2= u3= 3 м/с, m1=0,5, e=0,045; 2 - u1= u2= u3= 5 м/с, m1=0,5, e=0,045; 3 - u1= u2= u3= 7 м/с, m1=0,5, e=0,045; 4 - u1=5 м/с, u2= u3= 0 м/с, m1=0,5, t2=15 c, m2=0,6, e=0,045; 5 - u1= u2= u3= 7 м/с, m1=0,15, e=0,045; 6 - u1= u2= u3= 3 м/с, m1=0,5, e=0; 7 - u1= u2= u3= 5 м/с, m1=0,5, e=0; 8 - u1= u2= u3= 7 м/с, m1=0,5, e=0.
Известно, что при стационарном и равноускоренном режиме движения СВП [63,65,139] значение критической скорости зависит от глубины водоема.
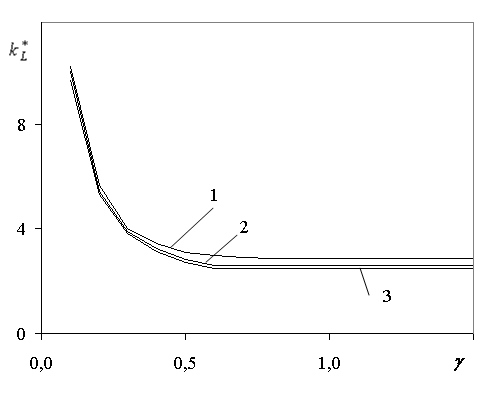
На рис.2.27 представлены результаты зависимости безразмерного коэффициента ![]() , соответствующего максимальному волновому сопротивлению при движении судна на первом режиме, от безразмерного параметра глубины водоема
, соответствующего максимальному волновому сопротивлению при движении судна на первом режиме, от безразмерного параметра глубины водоема ![]() . Видно, что с ростом параметра флотации
. Видно, что с ростом параметра флотации![]() и с уменьшением глубины водоема происходит смещение величины
и с уменьшением глубины водоема происходит смещение величины![]() в сторону меньших скоростей. Данные факты имеют место и для стационарного [65], и для равноускоренного движения СВП в битом льду [63] и на чистой воде [139].
в сторону меньших скоростей. Данные факты имеют место и для стационарного [65], и для равноускоренного движения СВП в битом льду [63] и на чистой воде [139].
 .
.
Рис.2.27. Зависимость безразмерного параметра критической скорости![]() от безразмерной глубины
от безразмерной глубины ![]() для различных
для различных ![]() : 1 - e=0,045; 2 - e=0,0225; 3 - e=0.
: 1 - e=0,045; 2 - e=0,0225; 3 - e=0.
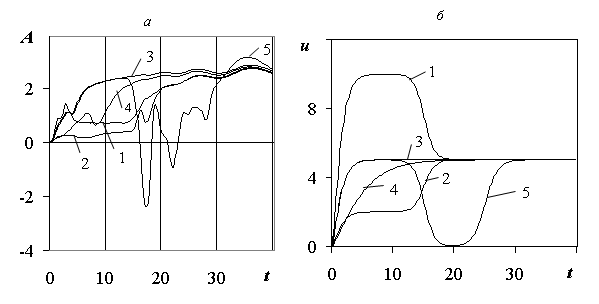
На рис. 2.28а-2.28б представлены зависимости волнового сопротивления и скорости судна от времени при различных выходах на критическую скорость через первый, третий, четвертый и пятый режимы движения для H=3 м, L=10 м,![]() , m2=0,6, t2=15 c. Здесь кривые 1 и 2 соответствуют выходу на критическую скорость через четвертый и третий режимы движения. Кривые 3 и 4 представляют волновое сопротивление при выходе на критическую скорость через первый режим движения с разными начальными ускорениями 2,5 м/с2 и 0,75 м/с2. Из анализа кривых 3 и 4 следует, что максимального волнового сопротивления легче и быстрее добиться при выходе на критическую скорость через первый режим движения с наибольшим ускорением. А при выходе на критическую скорость через третий и четвертый режимы движения (кривые 2 и 1) волновое сопротивление хотя и стремится к своему критическому значению, но уже не принимает максимальных значений, соответствующих данной критической скорости. Кривая 5 на рис. 2.28а представляет волновое сопротивление при выходе на критическую скорость через пятый режим движения. В данном случае выход судна на критическую скорость, затем торможение до нуля и повторный выход на критическую скорость позволяет добиться более высокого волнового сопротивления.
, m2=0,6, t2=15 c. Здесь кривые 1 и 2 соответствуют выходу на критическую скорость через четвертый и третий режимы движения. Кривые 3 и 4 представляют волновое сопротивление при выходе на критическую скорость через первый режим движения с разными начальными ускорениями 2,5 м/с2 и 0,75 м/с2. Из анализа кривых 3 и 4 следует, что максимального волнового сопротивления легче и быстрее добиться при выходе на критическую скорость через первый режим движения с наибольшим ускорением. А при выходе на критическую скорость через третий и четвертый режимы движения (кривые 2 и 1) волновое сопротивление хотя и стремится к своему критическому значению, но уже не принимает максимальных значений, соответствующих данной критической скорости. Кривая 5 на рис. 2.28а представляет волновое сопротивление при выходе на критическую скорость через пятый режим движения. В данном случае выход судна на критическую скорость, затем торможение до нуля и повторный выход на критическую скорость позволяет добиться более высокого волнового сопротивления.
 .
.
Рис.2.28. Зависимости волнового сопротивления СВПА (а) при различных режимах выхода СВПА на критическую скорость (б) для H=3 м, L=10 м,![]() , m2=0,6, t2=15 c: 1 – u1=10 м/с, u2= u3= 5 м/с, m1=0,5; 2 - u1=2 м/с, u2= u3= 5 м/с, m1=0,5; 3 - u1= u2= u3= 5 м/с, m1=0,5; 4 - u1= u2= u3= 5 м/с, m1=0,15; 5 - u1=5 м/с, u2=0 м/с, u3=5 м/с, m1=0,5, m3=0,5, t3=25с.
, m2=0,6, t2=15 c: 1 – u1=10 м/с, u2= u3= 5 м/с, m1=0,5; 2 - u1=2 м/с, u2= u3= 5 м/с, m1=0,5; 3 - u1= u2= u3= 5 м/с, m1=0,5; 4 - u1= u2= u3= 5 м/с, m1=0,15; 5 - u1=5 м/с, u2=0 м/с, u3=5 м/с, m1=0,5, m3=0,5, t3=25с.
Таким образом, анализируя полученные численные результаты, приведенные на рисунках 2.26-2.28, можно сделать следующие выводы. Максимальное волновое сопротивление при движении в битых льдах судно испытывает при движении с критической скоростью, значение которой зависит от глубины водоема, основных характеристик судна и битого льда. Для снижения волнового сопротивления рекомендуется двигаться на докритических скоростях либо выходить на заданную сверхкритическую скорость с максимальным ускорением.
При проведении ледокольных работ в целях разрушения берегового припая, дальнейшего измельчения битого льда или разрушения заторов и зажоров, представляющих собой нагромождения мелкобитого льда и являющихся причиной разрушительных наводнений, целесообразно применять режим движения СВП с максимальной крутизной волны. Для этого предлагается двигаться по следующим режимам движения:
§ выход на критическую скорость по первому режиму и движение на критической скорости;
§ выход на сверхкритическую скорость и затем плавное торможение до критической скорости;
§ выход на критическую скорость, затем торможение, и после того, как волна обгонит судно – повторный выход на критическую скорость.