
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
2.1.1.Простейшие механические модели вязкоупругого поведения
Упругие тела и вязкие жидкости существенно различаются своими свойствами при деформировании. Упругие деформируемые тела после снятия приложенных нагрузок возвращаются к своему естественному, или недеформированному, состоянию. В отличие от них несжимаемые вязкие жидкости совсем не имеют тенденции возвращаться после снятия нагрузки в исходное состояние. Кроме того, напряжения в упругом теле связаны непосредственно с деформациями, в то время как напряжения в вязкой жидкости зависят (за исключением гидростатической составляющей) от скоростей деформации.
Поведение материала, которое объединяет в себе оба эти свойства – и упругости, и вязкости, - называют вязкоупругим. Упругое тело и вязкая жидкость занимают крайние противоположные точки в широком спектре вязкоупругих сред.
Линейную вязкоупругость для одномерного состояния удобно трактовать при помощи механических моделей, которые наглядно демонстрируют поведение различных вязкоупругих материалов [93]. Эти модели строятся из таких механических элементов, как линейно-упругая пружина с модулем упругости E (массой этой пружины пренебрегают) и вязкий элемент (демпфер) с коэффициентом вязкости h (вязкий элемент представляет собой поршень, движущийся в цилиндре с вязкой жидкостью).

Рис. 2.1. Линейный упругий элемент
Как показано на рис. 2.1, сила s, растягивающая пружину, связана с ее удлинением e формулой
![]() . (2.1)
. (2.1)
Подобное же соотношение существует и для демпфера (рис. 2.2):
![]() (2.2)
(2.2)
где ![]() . Можно придать большую общность этим моделям и устранить размерные эффекты, если в качестве s рассматривать напряжение, а в качестве e - относительную деформацию.
. Можно придать большую общность этим моделям и устранить размерные эффекты, если в качестве s рассматривать напряжение, а в качестве e - относительную деформацию.


 .
.
Модель Максвелла вязкоупругого тела является комбинацией пружины и вязкого элемента (демпфера), соединенных последовательно (рис. 2.3).
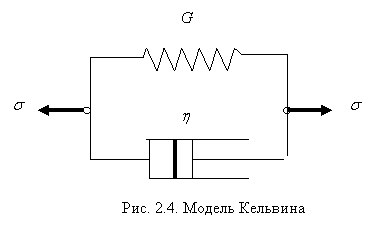
Модель Кельвина или Фойгта представляет собой параллельное соединение тех же элементов (рис. 2.4). Соотношение между напряжением и деформацией (фактически содержащее также и их скорости) для модели Максвелла дается формулой
 . (2.3)
. (2.3)
А для модели Кельвина соотношение между напряжением и деформацией задается формулой
![]() (2.4)
(2.4)
Эти уравнения являются по существу определяющими уравнениями вязкоупругости в одномерном случае.
Простые модели Максвелла и Кельвина не дают точного полного описания поведения реальных сред. Усложненные модели обладают большей гибкостью в отражении процессов в фактических материалах.
Рассмотрим четырехпараметрическую модель, состоящую из двух упругих и двух вязких элементов, представляющую собой последовательно соединенные узел Максвелла и узел Кельвина (рис. 2.5).
 .
.
Данная модель способна описать все три основных типа поведения вязкоупругой среды. Так, она объединяет в себя мгновенную упругую реакцию (за счет свободного элемента Gм), вязкое течение (за счет свободного вязкого элемента hм) и, наконец, запаздывающую упругую реакцию (за счет узла Кельвина).
Предполагается, что для описания вязкоупругих свойств плавающей ледяной пластины можно использовать данную линейную четырехпараметрическую модель.