
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 2.6. Квантовая статистика фермионов. Распределение Ферми-Дирака
В отличие от классических частиц для микрообъектов выполняется принцип тождественности или неразличимости частиц.
В соответствии с принципом тождественности, в любой системе при перестановке частиц одного сорта между различными состояниями, результат наблюдения остается прежним. Другими словами, если под «результатами наблюдений» понимать измеряемые в эксперименте вероятности, то тождественность, в первую очередь, относится к величине квадрата модуля Ψ-функции состояния системы микрообъектов, то есть к функции плотности вероятности.
Выберем в системе две частицы одного сорта, находящиеся в двух различных состояниях и поменяем их местами, не затрагивая остальных частиц, входящих в систему. Состояние системы, в котором первая частица характеризуется определенным набором параметров α (квантовыми числами), а вторая частица характеризуется другим набором параметров – β, формально можно записать следующим образом: Ψ(1α, 2β). После перестановки этих частиц состояние будет определено функцией Ψ(1β, 2α). Принцип тождественности теперь можно представить в виде равенства:
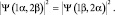 (2.6.1)
(2.6.1)
Этому равенству соответствует два независимых соотношения между функциями состояния:
1) Ψ(1α, 2β) = Ψ(1β, 1α), (функция четная): (бозоны),
2) Ψ(1α, 2β) = –Ψ(1β, 1α), (функция нечетная): (фермионы). (2.6.2)
Следовательно, как утверждается в первой строке (2.6.2), существуют микрообъекты такого сорта, что при их перестановке в системе, волновая функция не меняется (симметрия). Этот сорт частиц называется бозонами по фамилии индийского физика Бозе, исследовавшего вместе с Эйнштейном распределение бозонов по состояниям. Соответственно, на основе второго равенства, можно сделать вывод о существовании такого сорта микрообъектов, перестановка которых в системе меняет знак волновой функции на противоположный (антисимметрия). Этот сорт частиц называется фермионами по фамилии итальянского физика Фèрми, исследовавшего статистику фермионов. (Независимо от Ферми распределение фермионов по состояниям было изучено Дираком).
Такое деление микрообъектов оказалось связанным со спиновым квантовым числом: у бозонов проекция спина на выбранное направление Оz четная 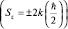 , а у фермионов – нечетная
, а у фермионов – нечетная 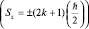 . Кратко говорят, что у бозонов спин целый, а у фермионов спин полуцелый.
. Кратко говорят, что у бозонов спин целый, а у фермионов спин полуцелый.
Для бозонов не существует запрета на возможность их совместного появления в одном состоянии. Действительно, если в равенстве (2.6.2) перейти к одному состоянию, то есть записать, что α = β, то это соотношение превратится в обычное тождество: Ψ(1α, 2α) = Ψ(1α, 1α).
Для фермионов, переход в одно состояние двух частиц приводит к другому соотношению: Ψ(1α, 2α) = –Ψ(1α, 1α). Функция равна сама себе с противоположным знаком может быть только в одном случае, когда она равна нулю. Отсюда следует, что 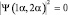 , то есть вероятность обнаружения в системе двух произвольно выбранных фермионов в одном и том же состоянии равна нулю. Последнее утверждение является одной из формулировок принципа запрета Паули для электронов в сложном атоме, для нуклонов в ядре, для кварков в адронах и т.п., то есть для микрообъектов с полуцелым спином в системе.
, то есть вероятность обнаружения в системе двух произвольно выбранных фермионов в одном и том же состоянии равна нулю. Последнее утверждение является одной из формулировок принципа запрета Паули для электронов в сложном атоме, для нуклонов в ядре, для кварков в адронах и т.п., то есть для микрообъектов с полуцелым спином в системе.
При распределении n-частиц в фазовом пространстве по Z ячейкам (состояниям) должно наблюдаться три различных распределения. Так например, для двух частиц, распределенных по двум ячейкам. будем иметь рис. 33.
Таким образом, должно существовать три различных статистики, одна из которых – для классических частиц – рассмотрена выше (распределение Максвелла-Больцмана).
Задача поиска распределений микрочастиц и вероятностей по энергиям составляет основу квантовых статистик. В общем виде функцию распределения по энергиям можно разбить на два распределения. Одно будет характеризовать распределение частиц или вероятностей по ячейкам фазового пространства, а другое – распределение самих ячеек по энергиям:
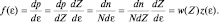 (2.6.3)
(2.6.3)
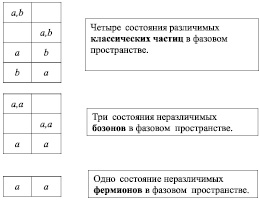
Рис. 33. Распределения двух частиц по двум состояниям
Вид функции w(Z), с точностью до постоянного нормирующего множителя, может иметь один и тот же вид зависимости от энергии и характеризовать: в одном случае, распределение вероятностей по состояниям с энергией ε, в другом случае, распределение частиц по состояниям с энергией ε, а в третьем – распределение концентрации частиц по состояниям с энергией ε:
 (2.6.4)
(2.6.4)
где 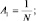
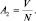
Одинаковым для бозонов и фермионов остается распределение ячеек по энергиям, так как эта функция не связана с самими частицами: 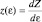 , поэтому поиск функции распределения начнем с z(ε).
, поэтому поиск функции распределения начнем с z(ε).
В фазовом пространстве микрообъекта размеры элементарного шестимерного кубика определяются произведением трех интервалов проекций импульса и трех интервалов проекций декартовых координат:
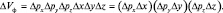 (2.6.5)
(2.6.5)
Конечная оценка минимальных размеров элементарного объема в фазовом пространстве сделана на основании соотношения неопределенностей Гейзенберга, которое характеризует наивысшую точность в определении проекций координат и импульсов микрообъекта и говорит о том, что дробить пространство далее бессмысленно, с точки зрения квантовой механики.
Пусть система частиц занимает в фазовом пространстве некоторый объем Vф. Тогда количество ячеек Z, занятых системой, легко вычислить делением общего объема на объем одной ячейки, а затем найти зависимость Z от энергии. При этом, подпространство импульсов изотропно и сферически симметрично, а подпространство координат Vкоорд определяет обычный трехмерный объем V, предоставленный в реальном пространстве системе микрообъектов. В результате имеем (при 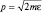 ):
):
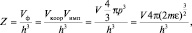
откуда, после взятия производной по ε, найдем искомое распределение ячеек по энергии:
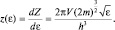 (2.6.6)
(2.6.6)
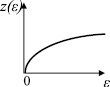
Рис. 34. График функции z(ε)
График полученной функции представлен на рис. 34. Для микрообъектов, обладающих ненулевым спином, количество состояний необходимо удвоить, так как в фиксированной системе координат направление спина таково, что его проекция на выделенное направление (например, на ось Oz) принимает две противоположных ориентации Sz = ±sħ. В этом случае в формулу (2.6.6) необходимо ввести поправку и она примет вид:
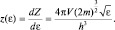 (2.6.7)
(2.6.7)
Динамическое равновесие для системы частиц (молекул) заключается в том, что при переходе частицы из одного микросостояния в другое меняется, в общем случае, и макросостояние системы, поэтому для сохранения равновесия необходимо, чтобы вероятность перехода системы из условно выбранного первого состояния во второе равнялась вероятности обратного перехода. Детальность принципа равновесия определяется тем, что анализируется одночастичный переход. В изолированной системе микросостояние частицы меняется при взаимодействии с другой частицей (взаимодействиями трехчастичными и более пренебрегаем, считая их редкими). Тогда наглядно можно представить ситуацию следующим образом (см. рис. 35).

Рис. 35. Два состояния системы
До взаимодействия частиц система находилась в состоянии I, а каждая из частиц занимала ячейку – микросостояние с энергией εi – c вероятностью w(εi). Выберем такие состояния двух частиц с энергиями ε1 и ε2, которые обязательно приводят к их взаимодействию в системе, в результате чего каждая из них оказывается в микросостояниях с энергиями ε3 и ε4, а система переходит в состояние II. Тогда переход из состояния I в состояние II возможен, если и первая ячейка будет «занята» частицей и вторая ячейка также будет занята другой частицей. Для фермионов недостаточным условием перехода является наличие частиц в первой и во второй ячейках, так как после взаимодействия частицы должны перейти в состояния не занятые другими частицами. В противном случае, принцип Паули запретит этот переход. Вероятности того, что ячейки с энергиями ε3 и ε4 свободны, равны, соответственно, [1 – w(ε3)] и [1 – w(ε4)]. Окончательно, вероятность перехода из состояния I в состояние II определится как произведение вероятностей совместных событий занятости первой и второй ячеек, а также незанятости третьей и четвертой ячеек. Аналогично, вероятность перехода системы в обратном направлении определится как произведение вероятностей занятости третьей и четвертой ячеек, а также вероятностей незанятости первой и второй ячеек. Тогда окончательно условие равновесия в системе PI→II = PII→I запишется следующим образом:
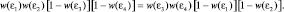 (2.6.8).
(2.6.8).
После деления левой и правой части на произведение четырех вероятностей w(ε1)∙w(ε2)∙w(ε3)∙w(ε4) получим:
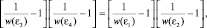
откуда после замены каждой из квадратных скобок, имеющих одинаковый вид, на функцию
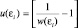 (2.6.9)
(2.6.9)
будем иметь следующее выражение: u(ε3)u(ε4) = u(ε1)u(ε2). Логарифмируя полученное выражение и учитывая закон сохранения энергии: сумма энергий частиц до взаимодействия и после взаимодействия сохраняется, будем иметь систему уравнений:
 (2.6.10)
(2.6.10)
После подстановки нижнего равенства в системе (1.8.3) в верхнее и взятия частной производной вначале по ε1, а затем по ε2, получим систему уравнений:
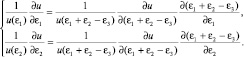 (2.6.11)
(2.6.11)
Крайние производные в правой части каждой строки равны единице, поэтому правые части равны, а следовательно, равны и левые части в (2.6.11):
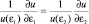 .
.
Последнее равенство двух функций от независимых переменных возможно только тогда, когда и левая, и правая части равенства равны одной и той же константе, которую обозначим β. Поэтому можно записать: 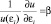 , откуда после разделения переменных u(εi) и εi, а затем последующего интегрирования, получим:
, откуда после разделения переменных u(εi) и εi, а затем последующего интегрирования, получим:
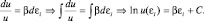
Потенцирование последнего равенства и применение последующих операций по замене функции u(εi) на функцию, зависящую от w(εi), после преобразований получим вид функции w(εi):
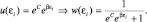 (2.6.12)
(2.6.12)
Как известно из квантовой механики (исходя из принципа соответствия) свойства микрообъектов совпадают со свойствами классических частиц при больших энергиях. Поэтому статистика фермионов при ε → ∞ должна совпадать со статистикой Максвелла-Больцмана (2.6.4). Действительно, при этих условиях, в знаменателе формулы (2.6.12) единицей можно пренебречь и с точностью до постоянного множителя обе статистики совпадут, если β = 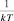 . Оставляя за этой постоянной такой же смысл, что и в классической статистике, введем
. Оставляя за этой постоянной такой же смысл, что и в классической статистике, введем 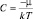 и преобразуем формулу (2.6.12) следующим образом:
и преобразуем формулу (2.6.12) следующим образом:
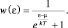 (2.6.13)
(2.6.13)
Как мы определили выше, величина w(ε) характеризует вероятность обнаружения фермионов в ячейке фазового пространства с энергией ε, то есть, другими словами, долю фермионов с энергией ε, находящихся в единице объема фазового пространства:
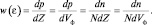
Построим график функции w(ε) при T = 0 K. Если ε > μ, w(ε) = 0. Это означает, что все состояния с ε > μ свободны.
При ε < μ, w(ε) = 1, а это означает, что все состояния с ε < μ заняты с вероятностью, равной единице. Если ε = μ, то в показателе экспоненты возникает неопределенность, которая означает «скачок» вероятности от 0 до 1. Поэтому, объединяя все результаты, получим вид функции w(ε), изображенный на рис. 36. Теперь можно определить физический смысл константы μ, как максимальной энергии фермионов при абсолютном нуле температур. Эта энергия была названа энергией Ферми. При нагревании система начинает поглощать тепловые фотоны с энергией hv << μ. Поэтому в теплоемкости могут участвовать только те частицы, энергия которых близка к μ, но доля которых мала. Действительно, переход фермиона (см. рис. 36) из состояния а в состояние b невозможен, так как оно уже занято с вероятностью 1, а переход из c в d разрешен, поскольку состояние d свободно. Таким образом, при нагревании уровень с энергией Ферми «размывается», так как справа от него заселенность уровней становится не равной нулю, а заселенность уровней слева – уменьшается. При Т ≠ 0 К и ε = μ вероятность w(ε) = 1/2 и вид графика несколько изменится (рис. 37).
Зная распределение частиц по состояниям (2.6.12) и распределение состояний по энергиям (2.6.6), получим распределение частиц и вероятностей по энергиям f(ε), перемножив функции z(ε) и w(ε):
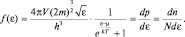 (2.6.14)
(2.6.14)
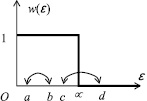
Рис. 36. График распределения фермионов по состояниям при Т = 0 К
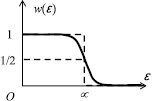
Рис. 37. График распределения фермионов по состояниям при Т ≠ 0 К
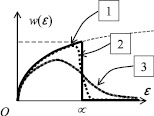
Рис. 38. График распределения фермионов по энергиям при Т = 0 К (1), Т ≠ 0 К (2-пунктир) и классических частиц (3)
Полученное выражение (2.6.14) представляет собой распределение Ферми – Дирака. Вид функций распределения по энергиям для фермионов при абсолютном нуле температур (1) и при Т ≠ 0 К (2) представлены на рис. 38. Эта функция показывает вероятность обнаружения у произвольно выбранного фермиона в фермионом газе энергии ε, величина которой попадает в единичный интервал значений энергии. Очевидно, что при увеличении температуры, фермионный газ будет распределен по энергиям таким же образом, как распределен классический газ. Поэтому возникает вопрос: при каких температурах рассматриваемый газ подчиняется статистике Максвелла-Больцмана, а при каких условиях его нельзя считать классическим, то есть он является газом из тождественных, «вырожденных» частиц и подчиняется квантовой статистике Ферми-Дирака? Используя принцип соответствия Бора, при 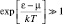 , единицей можно пренебречь и формула (2.6.14) станет соответствовать распределению Максвелла-Больцмана, то есть описывать классический газ. Очевидно, что при
, единицей можно пренебречь и формула (2.6.14) станет соответствовать распределению Максвелла-Больцмана, то есть описывать классический газ. Очевидно, что при 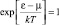 , единицей пренебречь невозможно и газ должен подчиняться распределению Ферми-Дирака. Это произойдет при условии выполнения равенства:
, единицей пренебречь невозможно и газ должен подчиняться распределению Ферми-Дирака. Это произойдет при условии выполнения равенства: 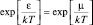 . Стоящая справа величина при постоянной температуре является константой, поэтому ее можно выбрать в качестве критерия перехода статистики в квантовую, если принять:
. Стоящая справа величина при постоянной температуре является константой, поэтому ее можно выбрать в качестве критерия перехода статистики в квантовую, если принять:
 (2.6.15)
(2.6.15)
Исходя из этого критерия вырождения газа, можно вычислить соответствующую температуру, при которой газ остается вырожденным и понадобится значительно увеличить температуру системы, то есть температуру условий, в которых будет находиться этот газ, чтобы распределение стало распределением для классических частиц. Вычислим вначале концентрацию частиц с энергией ε, для чего воспользуемся формулой распределения (2.6.14), поделив левую и правую части равенства на объем:
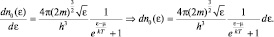
Интегрируя полученный результат по величине энергии, будем иметь концентрацию всех частиц независимо от их энергии:
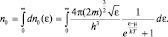 (2.6.16)
(2.6.16)
Интересующая нас величина 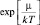 не зависит от энергии, поэтому для ее оценки можно еще раз воспользоваться переходом в классическую статистику и пренебречь единицей в знаменателе дроби в подынтегральной функции. В результате получим следующее выражение:
не зависит от энергии, поэтому для ее оценки можно еще раз воспользоваться переходом в классическую статистику и пренебречь единицей в знаменателе дроби в подынтегральной функции. В результате получим следующее выражение:
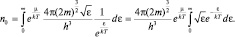
После замены переменных 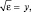 ε = y2, dε = 2yay интеграл становится табличным (см. 1.4.3):
ε = y2, dε = 2yay интеграл становится табличным (см. 1.4.3):
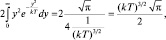
используя решение которого и предыдущее равенство, получим: 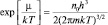 . Так как ранее было определено, что критерий вырождения должен равняться единице (cм. (2.6.15)), то соответствующая условию вырождения температура, называемая температурой Ферми, вычисляется следующим образом:
. Так как ранее было определено, что критерий вырождения должен равняться единице (cм. (2.6.15)), то соответствующая условию вырождения температура, называемая температурой Ферми, вычисляется следующим образом:
 (2.6.17)
(2.6.17)
Рассмотрим конкретный пример для оценки температуры вырождения. На гексагональную ячейку кристаллического двухвалентного цинка (3d104s2) объемом V = 30∙10–30 м3 приходится 12 свободных электронов. Следовательно, концентрация частиц равна n0 = 4∙1029 м–3. Отсюда, производя вычисления по формуле (2.6.17), получим величину температуры вырождения равную TF = 50000 K. При нормальных условиях (T = 300 K) следует считать, что эта температура близка к абсолютному нулю, так как 300 K << 50000 K. Поэтому, при нормальных условиях электронный газ в металлах является вырожденным и к расчету характеристик этих веществ (удельное сопротивление, коэффициент теплопроводности и др.) нельзя применять классическую статистику Максвелла-Больцмана.
При нагревании до температур выше TF, как этого требует переход к классике, вещество превратится в плазму. Для того чтобы можно было применять классическую статистику, необходимо резко понизить температуру Ферми, что можно сделать, если в веществе значительно снизится концентрация частиц или сами частицы станут значительно «тяжелее», то есть возрастет их масса. Практически, первое требование выполнимо для полупроводников с p- или n-проводимостью, обусловленной дефектами структуры твердого тела, а второе – выполняется для веществ с ионной проводимостью.
Для однородного и изотропного газа легко изобразить в фазовом подпространстве импульсов граничную поверхность, соответствующую энергии Ферми. Действительно, величина максимального импульса фермионов при температурах близких абсолютному нулю определится из равенства: 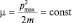 . Очевидно, что в сферически симметричном пространстве импульсов образуется поверхность с радиусом pmax, которая называется поверхностью Ферми. Симметрия кристалла определяет анизотропию его свойств и поэтому для анизотропной среды форма поверхности Ферми может иметь самый причудливый вид. Так, например, в случае рассмотренного выше электронного газа в кристаллах цинка, ячейка которого принадлежит к гексагональной симметрии, форма Ферми – поверхности отражает эту симметрию оси шестого порядка. В частности, проводимость монокристалла в различных направлениях разная и это позволяет экспериментально получить структуру поверхности и использовать ее характеристики для теоретических расчетов характеристик, описывающих другие свойства, для экспериментального анализа которых существуют значительные трудности.
. Очевидно, что в сферически симметричном пространстве импульсов образуется поверхность с радиусом pmax, которая называется поверхностью Ферми. Симметрия кристалла определяет анизотропию его свойств и поэтому для анизотропной среды форма поверхности Ферми может иметь самый причудливый вид. Так, например, в случае рассмотренного выше электронного газа в кристаллах цинка, ячейка которого принадлежит к гексагональной симметрии, форма Ферми – поверхности отражает эту симметрию оси шестого порядка. В частности, проводимость монокристалла в различных направлениях разная и это позволяет экспериментально получить структуру поверхности и использовать ее характеристики для теоретических расчетов характеристик, описывающих другие свойства, для экспериментального анализа которых существуют значительные трудности.
