Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 1.5. Основные принципы квантовой механики
Теперь сформулируем основные принципы квантовой механики.
1. Существует Ψ-функция состояния микрообъектов, удовлетворяющая стандартным требованиям, являющаяся решением уравнения Шредингера и имеющая тот смысл, что квадрат ее модуля определяют функцию плотности вероятности, т.е. вероятности обнаружения микрообъекта в единичном интервале возможных состояний.
2. Существует набор функций состояний (базис), определяющий все возможные независимые состояния, удовлетворяющие принципу суперпозиций: если квантовомеханическая система может находиться в состоянии Ψi и в состоянии Ψj, то она может находиться и в состоянии:
Ψ = ciΨi + cjΨj. (1.5.1)
Действительно, так как и Ψi и Ψj удовлетворяют уравнению Шредингера, то и их линейная комбинация также есть решение уравнения.
Важно отметить, что подобные соотношения характерны для векторов. Поэтому, полный набор линейно независимых волновых функций {Ψi} образуют базис комплексного (Гильбертова) пространства.
Следствие: Волновая Ψ-функция состояния системы удовлетворяет условиям нормировки и ортогональности:
,
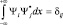где δij – символ Кронекера.
3. Принцип соответствия (предложен Н. Бором). Вначале остановимся на методологической формулировке этого принципа, впервые сформулированного Н. Бором: всякая новая теория (квантовая механика) содержит старую (классическую механику) как частный, предельный случай. Вообще говоря, это характерно не только для квантовой и классической механики, но и для отношений классической механики и СТО. В последнем примере, легко видеть, что при скоростях движения объектов, соизмеримых со скоростью света в вакууме, преобразования Лоренца переходят в преобразования Галилея со всеми вытекающими последствиями.
Как отыскать условия перехода от квантовых представлений к классическим? Новыми фактами по сравнению с обычной механикой являются квантовые «скачки» в атоме водорода (а) и соотношения неопределенностей (б), записанные ниже:
(а) 
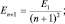
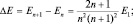
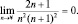
Вывод: при переходах атома из одного состояния в другое с большими квантовыми числами изменение энергии ΔΕ → 0, т.е. практически все эти переходы совершаются «квазинепрерывно».
(б) ΔxΔpx ≥ ħ при 
приводит к тому, что 
и 
, а тогда Δx и Δpx могут одновременно обратиться в нуль, а x и px примут точные значения. Поэтому, считая ħ = 1,05∙10–34 Дж∙с малой величиной, неопределенности «исчезают» и результаты вычислений квантовой и классической механики совпадут.
Принцип соответствия можно расширить также следующим образом: каждой величине классической механики соответствует оператор квантовой механики и при этом действия над операторами в квантовой механике подобны действиям над величинами в классике. В этом мы уже убедились раньше.
4. Принцип дополнительности. Этот принцип также предложен и разработан Н. Бором и имеет несколько формулировок:
а) волновые свойства микрообъектов являются дополнительными к квантовым свойствам и совместно определяют его поведение (корпускулярно-волновой дуализм);
б) так как координаты и импульсы микрообъектов нельзя измерить одновременно, то описание поведения можно вести либо на основе координатного базиса, либо на основе импульсного, которые и являются по отношению друг к другу дополнительными.
Перечисленными принципами мы будем руководствоваться при решении конкретных задач квантовой механики. Но прежде, чем приступить к этим задачам, необходимо разработать наглядные модели явлений и процессов в микромире. С одним из типов наглядных моделей в физике мы уже познакомились в школьном курсе физики – это изображение диаграммы (схемы) энергетических уровней атома водорода в боровской модели. Он чаще всего используется в спектральном анализе различных веществ и физике твердого тела (зонной теории).
Второй способ моделирования – изображение функции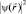 
в пространстве. Этот способ «взяли на вооружение» специалисты по структурному анализу вещества, физики твердого тела, кристаллографии, квантовой химии, молекулярной биологии для анализа химических связей (типы связей, направленности, симметрии и т.п.). мы будем заниматься этим после решения некоторых задач, т.к., чтобы изображать функцию, необходимо ее сначала вычислить.
Наконец, третий способ (используемый чаще всего в физике твердого тела) – это построение потенциальных кривых, которые характеризуют взаимодействие системы с внешними полями. Рассмотрим использование этого метода на нескольких примерах.
1. Осциллятор. Потенциальная энергия при наличии упругих («квазиупругих») сил имеет вид: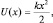 
k – коэффициент упругости. Потенциальная кривая U(x) имеет вид параболы (рис. 4). Если речь идет о состоянии стационарного движения осциллятора, то полная энергия
2. Электрон в кулоновском поле ядра атома (иона). Потенциальная энергия связи в этом случае имеет вид гипербол, расположенных симметрично относительно оси OU:
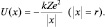
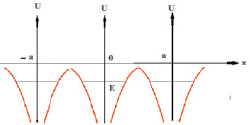
Рис. 5. Потенциальные ямы для электрона в одномерной кристаллической решетке
График функции изображенный на рис. 5. для кристаллической решетки, в узлах которой расположены положительные ионы, имеет вид потенциальных «ям». Центральная часть графика относится к системе ион-электрон и представляет собой «бесконечно глубокую потенциальную яму».
3. Ионная (гетерополярная) связь. Пусть имеем систему типа Na+ + Cl– в твердой фазе. Для выяснения зависимости величины взаимодействия от расстояния атомов или молекул в веществе достаточно проделать небольшой эксперимент с обычной резинкой по ее растяжению и сжатию (с твердым телом экспериментировать сложнее). Легко делается вывод, что на больших расстояниях (растягиваем резинку) преобладает энергия притяжения, а на малых (при сжатии) энергия отталкивания. Поэтому, если считать потенциальную энергию связи отрицательной и учесть кулоновский характер взаимодействия, то можно записать зависимость потенциальной энергии от расстояния:
U = U1 + U2,
где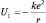 
– энергия кулоновского притяжения ионов, а 
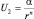– энергия электростатического отталкивания электронных облаков. Как видно из графика, r0 – расстояние в системе NaCl, где энергии отталкивания и притяжения скомпенсированы. Показатель степени n ≥ 2, т.к. в противном случае (при n < 2) отталкивание не смогло бы преобладать на малых расстояниях. Ясно также, что значение величины показателя должно зависеть от конкретного устройства атомов и молекул. Не вдаваясь в «технику» расчета, которая не принципиальна, воспользуемся готовым результатом, где для связи Na+–Cl– n = 5. Тогда результат притяжения и отталкивания можно представить как сумму этих взаимодействий:
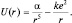
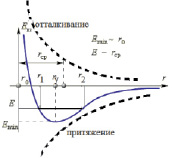
Рис. 6. Межмолекулярное взаимодействие (гетерополярная связь)
Межмолекулярное взаимодействие лежит в основе работы атомно-силового микроскопа (АСМ), позволяющего исследовать структуру вещества. С помощью очень тонкой иглы и «кантилевера», на котором она находится, исследуется поверхность материала методом сканирования. Все шероховатости меняют величину взаимодействия иглы с молекулами поверхности, и это приводит к деформации кантилевера. Эти деформации фиксируются либо с помощью пьезоэффекта, либо лазерным лучом. На рис. 7 представлен вид пористой поверхности анодированного оксида алюминия, полученной с помощью этого микроскопа.
Возвратимся к анализу ионной связи в кристаллах поваренной соли. Вид функций: отталкивание – U1(r), притяжение – U2(r) и U(r) представлены на рис. 6.
При температуре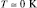 
кристалла NaCl движение Cl– происходит с минимальной скоростью и кинетическая энергия 
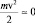. Тогда полная и потенциальная энергия совпадают, т.е. E0 = Umin (наиболее устойчивое состояние и r = ry). При увеличении энергии тела (нагревание) E > Umin и в точках r1 и r2 совпадает с потенциальной энергией. В этих точках Cl– покоится относительно Na + и не может двигаться в сторону r < r1 и r > r2; 
будет характеризовать среднее расстояние в системе. Нетрудно видеть, что при нагревании тела 
смещается вправо по оси r (тела при нагревании рас- ширяются).
4. α-Частица и ядро. Для α-частицы вне ядра на расстояниях r > R0 характерно кулоновское отталкивание: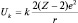 
. Внутри ядра, состоящего из протонов и нейтронов, положительно заряженная α-частица в среднем имеет одинаковое окружение нуклонами, а поэтому, считая ядерное взаимодействие короткодействующим, делаем вывод, что при r < R0, Uβ(r) = const.
Для стабильных ядер энергия связи в ядре между ее частицами по модулю гораздо больше кулоновского взаимодействия, поэтому U(r) = Umin < 0.
Если же α-частица располагается у границы ядра, т.е. при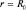 
, ядерные и кулоновские силы становятся соизмеримыми. Энергия связи 
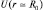резко изменяется. В результате имеем потенциальную кривую, представленную на рис. 8. Вид кривой позволяет ввести термины: «потенциальный ящик» (при r < R0), «потенциальный барьер» (при r = R0) и «высота потенциального барьера» Umax. Так, например, для ядра радиоактивного элемента Ra, излучающего α-частицы, 
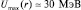, кинетическая энергия α-частицы вдали от ядра составляет 
.