Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Теоретические основы водного транспорта леса

Корпачев В. П.,

6.3 Математическая модель волны

При рассмотрении математической теории волн принимаем, что в жидкости отсутствуют силы вязкости, жидкость однородная, движение потенциальное. Давление на свободной поверхности жидкости в точках, определяемое координатой x (рисунок 6.2), равно атмосферному; на свободную поверхность действует только ветровое возмущение; дно горизонтальное и непроницаемое. Начало координат принимаем на плоскости, совпадающей с поверхностью покоящейся жидкости. Ось z направлена вверх.

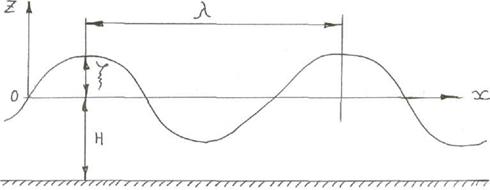
Рисунок 6.2 Профиль волны

Предположение о потенциальности волнового движения позволит свести задачу исследования волнового процесса к нахождению потенциала скорости j (x, y, z, t) этого течения, который в данном случае представляет собой функцию координат точек пространства, занятого жидкостью, и времени.

Для потенциального движения справедлив интеграл Лагранжа в форме

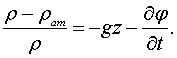  (6.1)

Значение потенциала j позволяет вычислить все характеристики волнового движения, поле скорости и давления. Потенциал для выбранной системы координат (рисунок 6.2) может быть определен из уравнения Лапласа

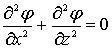  (6.2)

при граничных условиях, соответствующих рассматриваемому движению. Первое пограничное условие заключается в постоянстве давления на свободной поверхности и его равенстве атмосферному давлению Р_ат

Р = Р_ат = const. (6.3)

Учитывая, что x представляет собой превышение точек свободной поверхности волны над их положением в состоянии покоя (рисунок 6.2), из уравнения (6.1) получим первое пограничное условие на свободной поверхности волны в виде

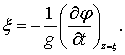  (6.4)

Второе пограничное условие на свободной поверхности волны заключается в следующем.

Координата x = f (t, x) вертикальная составляющая w скорости течения

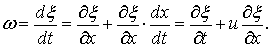  (6.5)

В волнах малой высоты υ < U (U - скорость движения частиц жидкости) ¶x/¶x мала, поэтому величиной ¶x/¶x можно пренебречь. Тогда из выражения (6.5) получим

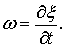
Вертикальная составляющая w скорости течения имеет при потенциальном движении и другое значение w = ¶j/¶z.

Следовательно,

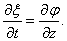  (6.6)

Дифференцируя (6.6) по t, получим:

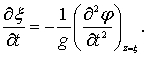  (6.7)

Приравнивая правые части уравнений (6.6) и (6.7), получим второе пограничное условие на свободной поверхности волны в виде

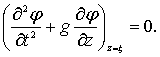  (6.8)

При z = -H, т.е. на горизонтальном дне частицы жидкости в волне, лежащие на дне, перемещаются только горизонтально

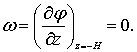  (6.9)

В случае H = ¥

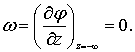  (6.10)

Опыт показывает, что потенциал скорости в бегущих волнах j (x, z, t) можно представить в виде произведения двух величин, одна из которыхz = f(z) является функцией только координаты z, а другая - периодической функцией только координаты x и времени t в форме функции f(x, t)=sinθ, где θ– некоторый угол, определяемый формулой

θ = k x – σ t,  (6.11)

где   σ – угловая скорость;

 t – время;

 k – постоянная величина,связанная с длиной волны и называется волновым числом. Оно показывает, какое число длин волн укладывается на отрезке 2π.

С учетом сказанного можно записать

j = z sin θ = z sin (k x - σ t)  (6.12)

Уравнение Лапласа принимает вид:

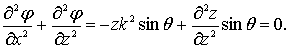  (6.13)

Считая, что sin ¹ 0, получим  линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами

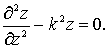  (6.14)

Решение этого уравнения имеет вид:

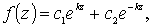  (6.15)

где  c₁, c₂ – постоянные интегрирования.

Подставляя в формулу (6.12) значение z (6.15), получим выражение для потенциала скорости

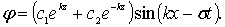  (6.16)

В формуле (6.16) величина sin(k x – σ t) определяет периодичность изменения функции j в течение периода τ в точках каждой вертикали. Значение постоянных интегрирования c₁ и c₂ определяются в соответствии с заданными пограничными условиями.